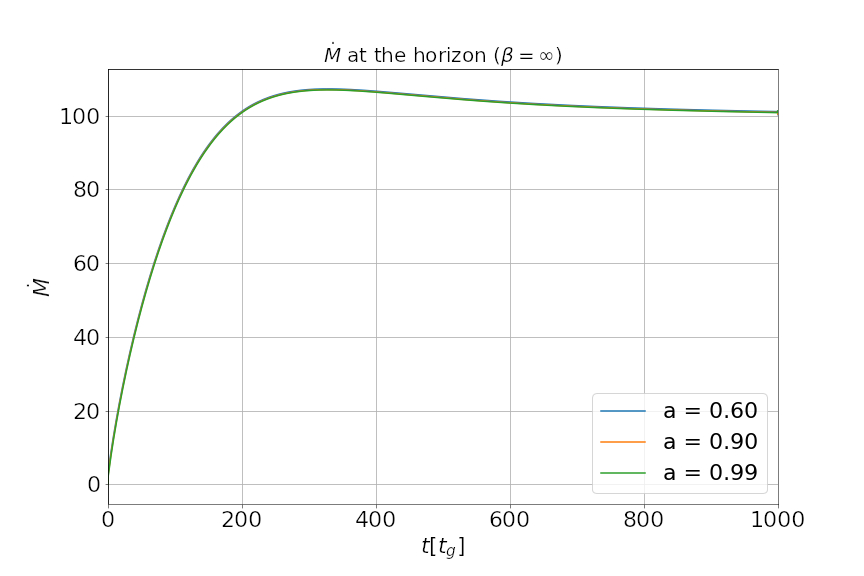
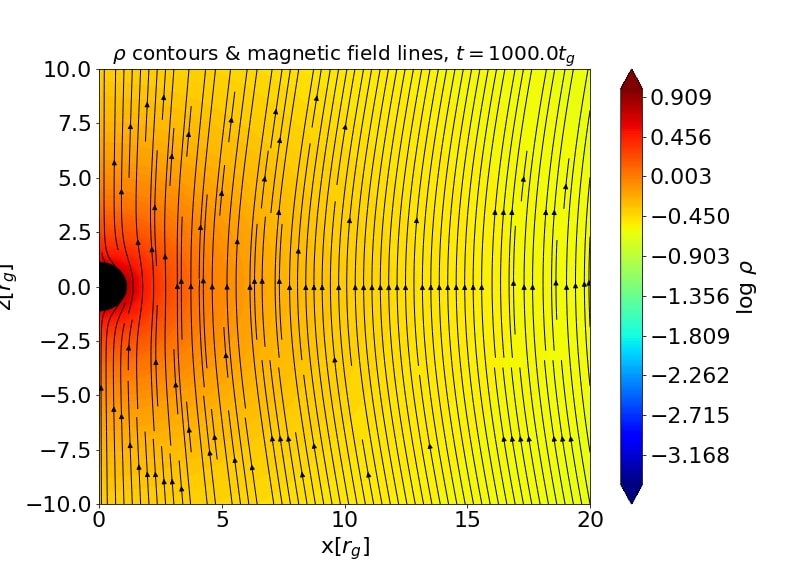
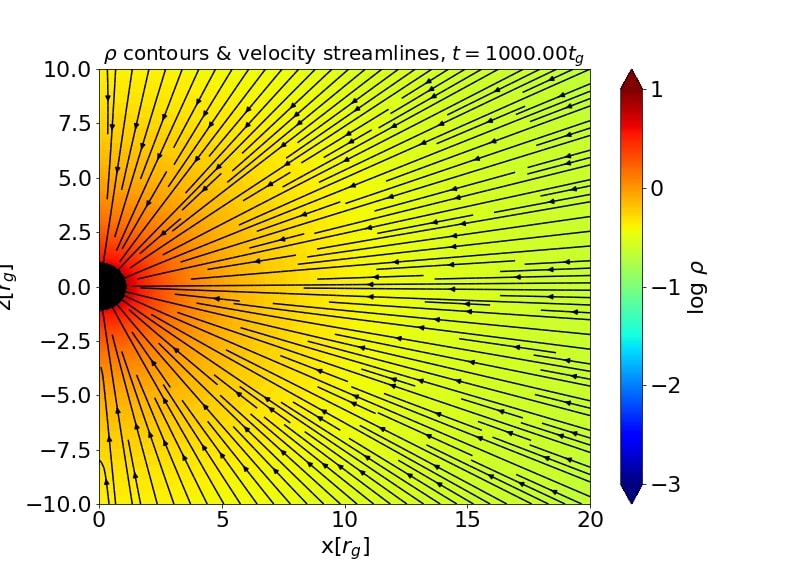
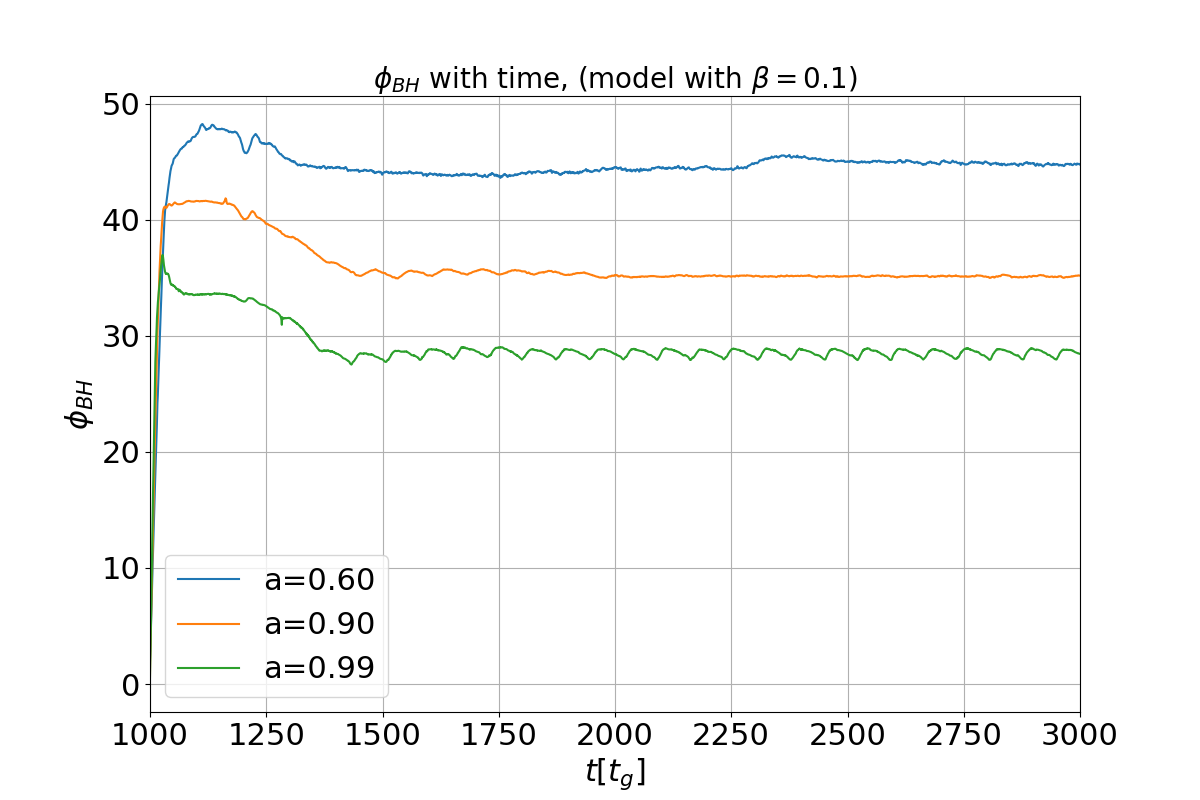
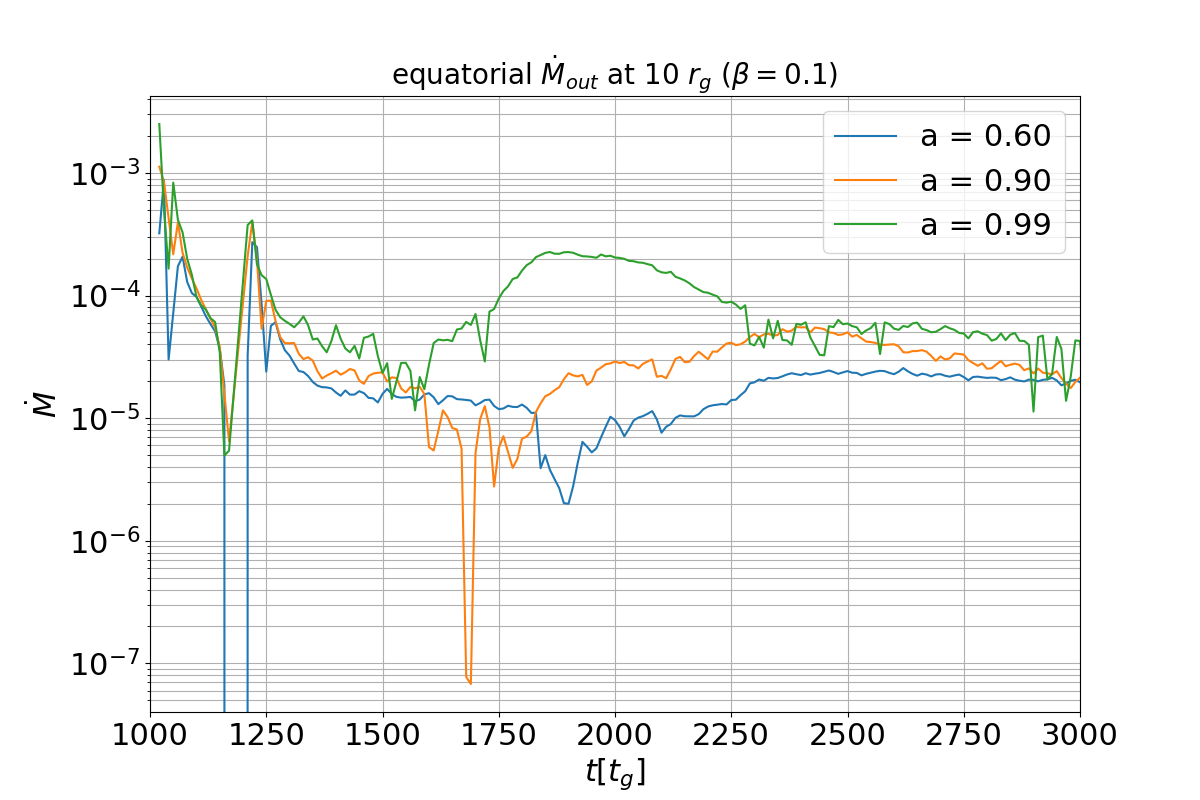
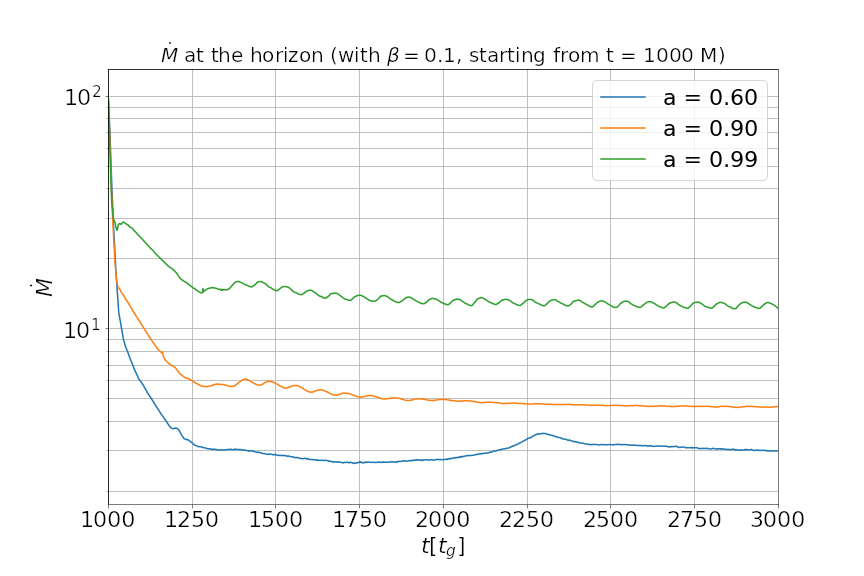
Various observational studies point towards the idea that an accreting black hole acts as the central engine of astrophysical objects such as active galactic nuclei (AGN) and gamma-ray bursts. The accretion of plasma onto the central compact object due to its gravitational force produces various observable effects including the relativistic jets and outflows in the form of winds. It is appropriate to assume that plasma at large-scales is magnetized due to its environment. In this work we focus on the equatorial outflows in an accreting plasma around a central black hole mediated by the presence of large-scale magnetic fields. Such outflows are recently considered to explain the observed properties of M87*, with an in-fall of matter at a larger radius and an ejection disc at a smaller radius [1]. In this work we are interested in gradually evolving the structure of the magnetic field and mass flow in the regions near to the black hole horizon in the presence of a large-scale uniform magnetic field (Wald, 1974) [2]. We use an initially spherically symmetric inflow, given by the Bondi (1952) solution [3], as the initial stationary solution and evolve it with time.

Outflows initiated by magnetically modified spherical accretion onto black hole

- 1 Center for Theoretical Physics Polish Academy of Sciences, Warsaw
- 2 Astronomical Institute of the Czech Academy of Sciences, Prague