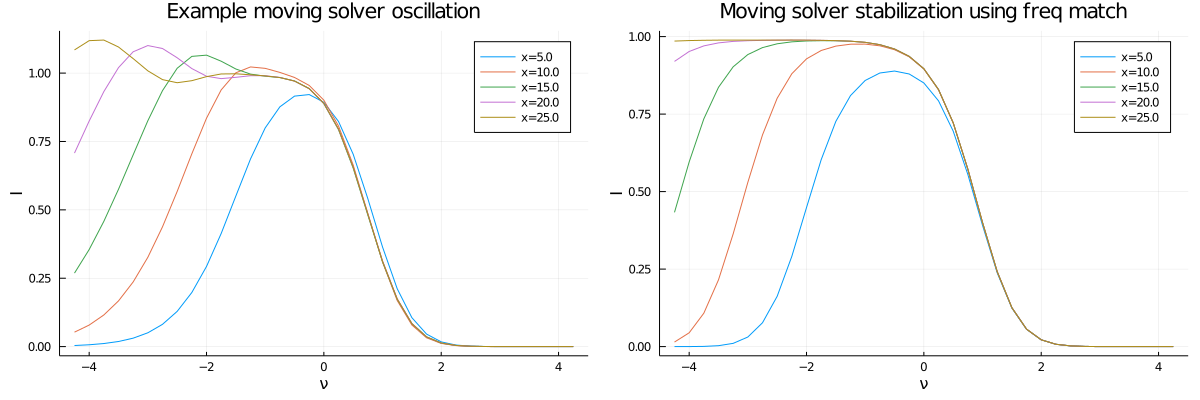
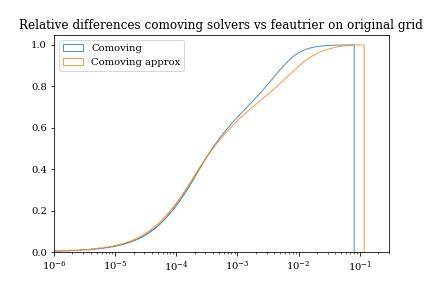
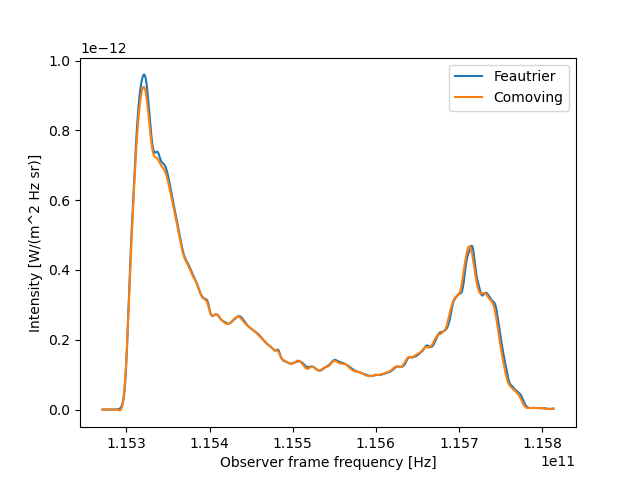
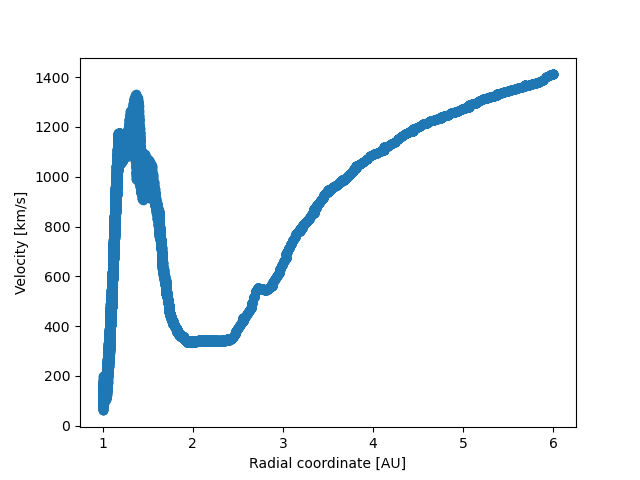
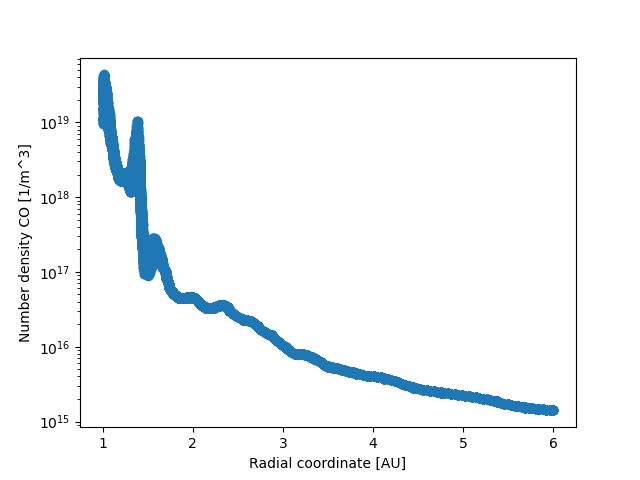
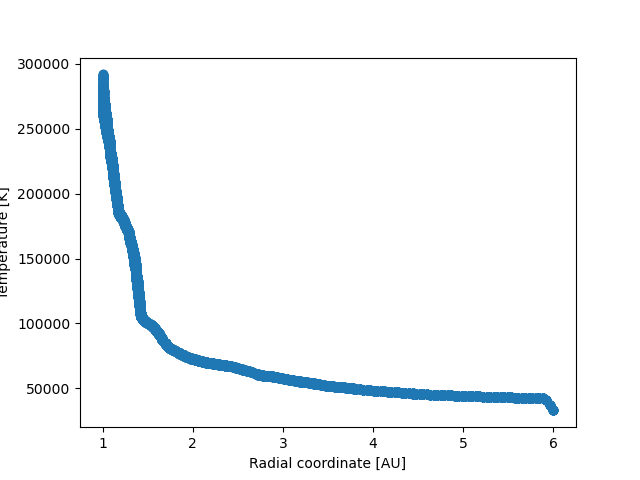
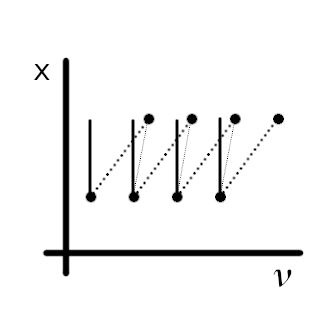
In line radiative transfer, the intensity at a specific frequency changes when that frequency is in the neighborhoud of an atomic/molecular line. Due to Doppler shifts, this region moves in frequency space if the velocity changes.
Using the default radiative transfer equation on a ray,
does not allow for a change in the frequency 𝜈. Thus computation time will be spent computing intensities in frequency regions where the intensity does not significantly change.
For computational efficiency, we propose a slight alteration of the radiative transfer equation.
This formulation allows for a change in frequency when solving this equation.
I exploit this feature in two applications:
- Computing NLTE intensities for line radiative transfer: The radiative properties of the medium depend on the radiation field at frequencies near the (Doppler shifted) line frequencies.
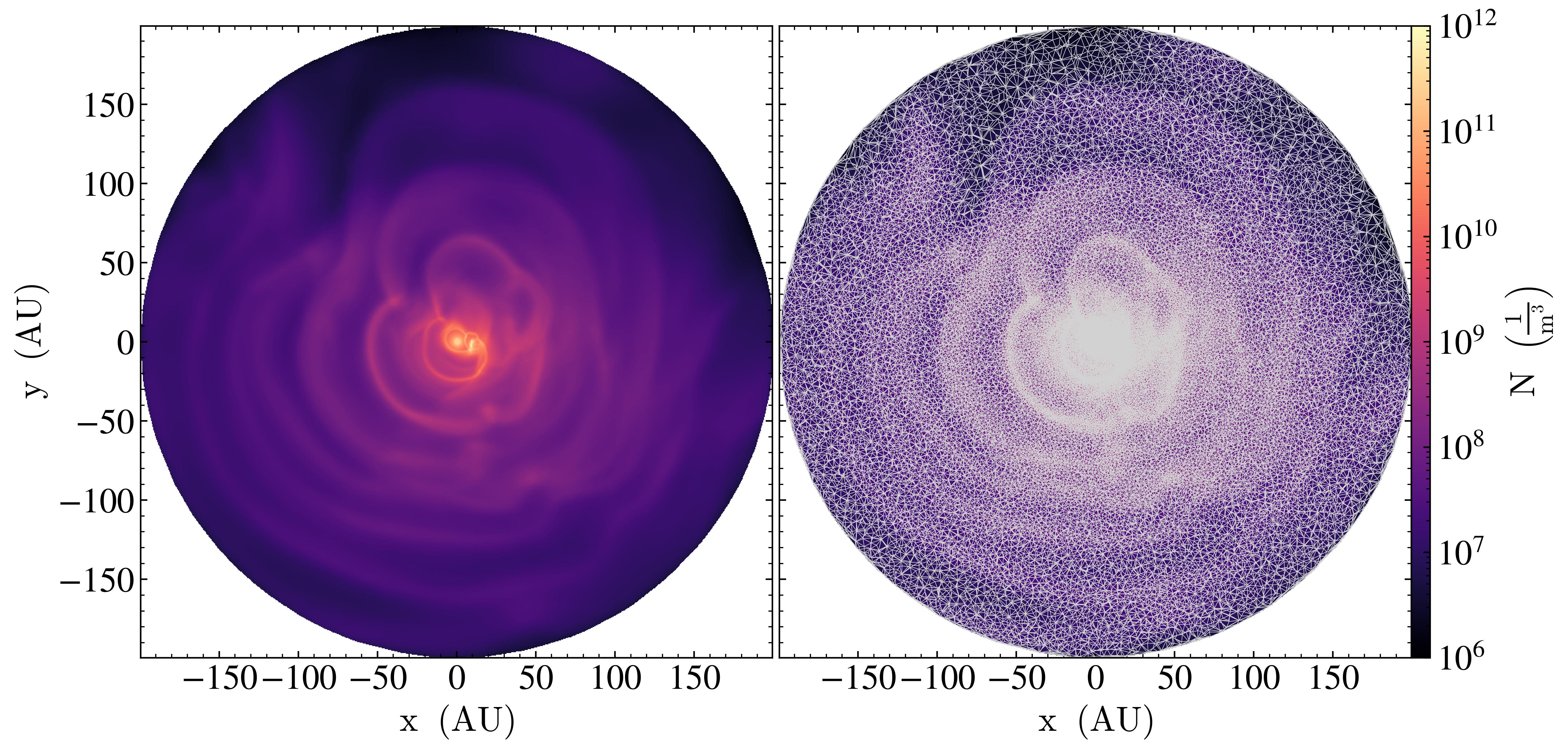
- Imaging models with non-monotonic velocity gradients: Both a wide frequency range and a fine frequency distribution is required for the line profile.
This comoving description of the radiative transfer equation similar to Baron & Hauschildt 2004 (and others in the same series). This poster adds the following improvements:
- A novel way to stabilize the equations
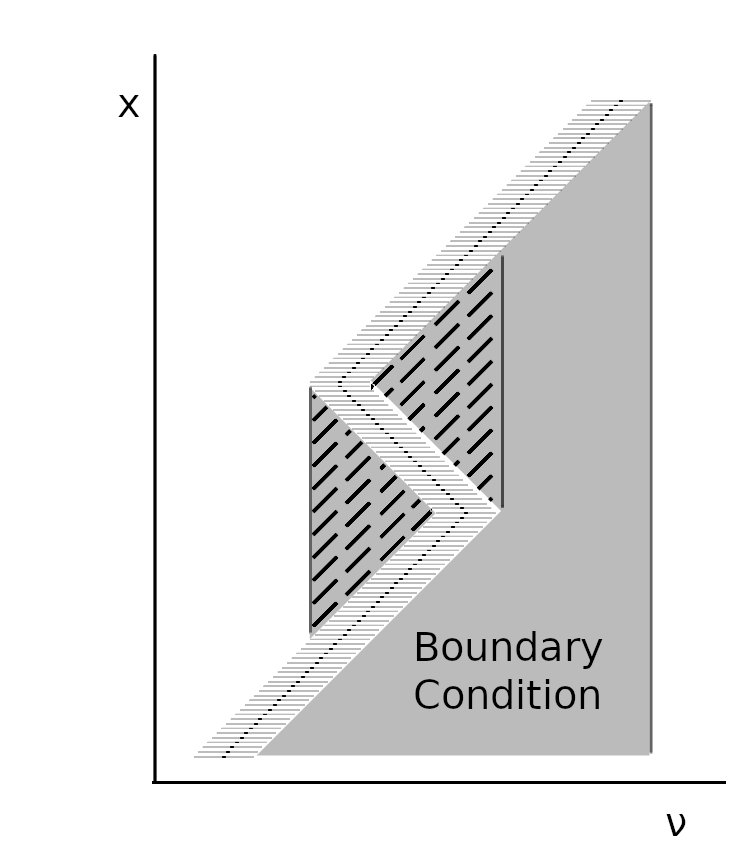
- Implementation of accurate boundary conditions which support non-monotonic velocity gradients