Fast emulation of full-sky anisotropies induced in the cosmic microwave background by cosmic strings

Abstract

Cosmic strings are linear topological defects that may have been produced during symmetry-breaking phase transitions in the very early Universe. In an expanding Universe the existence of causally separate regions prevents such symmetries from being broken uniformly, with a network of cosmic strings inevitably forming as a result. To faithfully generate observables downstream from such processes requires highly computationally expensive numerical simulations, which prohibit many modern analysis techniques. One may instead emulate observables, thus circumventing simulation.

Emulation is a form of generative modelling, often build upon a machine learning backbone. End-to-end emulation can often fail due to a combination of high dimensionality and insufficient training data. Consequently, it is common to instead emulate a latent representation from which observables may readily be synthesised. Scattering transforms and wavelet phase harmonics have emerged as excellent latent representations for cosmological fields, both as summary statistics and for emulation, since they do not require training and are highly sensitive to non-Gaussian information.

Leveraging wavelet phase harmonics as an intermediate latent representation, we develop techniques to emulate synthetic string induced CMB temperature anisotropies over a 7.2 degree field of view (FoV), with a sub-arcminute resolution in under a minute on a single NVIDIA A100 GPU. These synthetic maps are validated against a broad set of summary statistics and we find they are in excellent statistically agreement with comprehensive Nambu-Goto simulations, which require over a day of compute to generate.

In many cases observations are made over a limited region of the sky only and so the emulation techniques we present above are applicable and highly effective. For the paradigm of wide-field observations where observations are made over the majority of the celestial sphere (e.g. Planck, Stage IV lensing surveys), spherical methods are necessary. To this end, we have developed automatically differentiable and accelerated spherical harmonic, Wigner, and spherical wavelet transforms, which we make publicly available. These transforms are sampling agnostic and have core support for a variety of schemes, e.g. HEALPix. Building on these foundational tools, we have developed various spherical scattering representations, which we use to emulate high-resolution, high-fidelity cosmic string networks over the celestial sphere. Until now, such simulations have required hundreds of thousands of CPU hours of compute, hence the development of fast emulation techniques opens the door to a plethora of modern analysis techniques to search for the existence of cosmic strings.

Generative modelling

Generative modelling of physical fields

Generative modelling is a term broadly ascribed to the generation of synthetic observables that approximate authentic observables. A diverse range of generative models exist with varying motivations, although many are motivated by the manifold hypothesis (Bengio et al. 2013).

Simulation

Classically, physicists have attempted to encode the dynamics of a physical system, evolving some initial conditions over time to late universe observables. Provide the physics is faithfully codified, the resulting observables will faithfully represent authentic observables. The primary drawback of simulation is computational complexity: as we become interested in increasingly finer scale effects, the computational requirement to run such simulations become entirely infeasible.

Latent Emulation

Recently, researchers have instead attempted to map directly from cosmological parameters to late universe observables, circumventing the need for large-scale simulations. To model such complex mappings one may normally adopt machine learning techniques, however in many cases existing data on which to train such models does not exist. Therefore, conventional machine learning methods are impractical to train.

Instead, we adopt bespoke rather than learned statistical representations from which field level realisations may readily be synthesised (Price et al. 2023). One such class of representations are that of wavelet scattering transforms (Mallat et al. 2012, Allys et al. 2019, Mousset et al. 2023) which capture significant complex non-Gaussian structural information of signals.

Latent emulation is a multistep process:

Compute the scattering representation of a true (or faithfully simulated) field. These statistics will be our target.
Generate a random noise field to ensure we begin in the maximum entropy state.
Leverage automatic differentation to update this field such that its statistics match our desired target.

In this way, one may rapidly generate many different realisations of physical fields from a single input, or perhaps a limited ensemble of inputs. In essence, this could be considered extreme data augmentation.

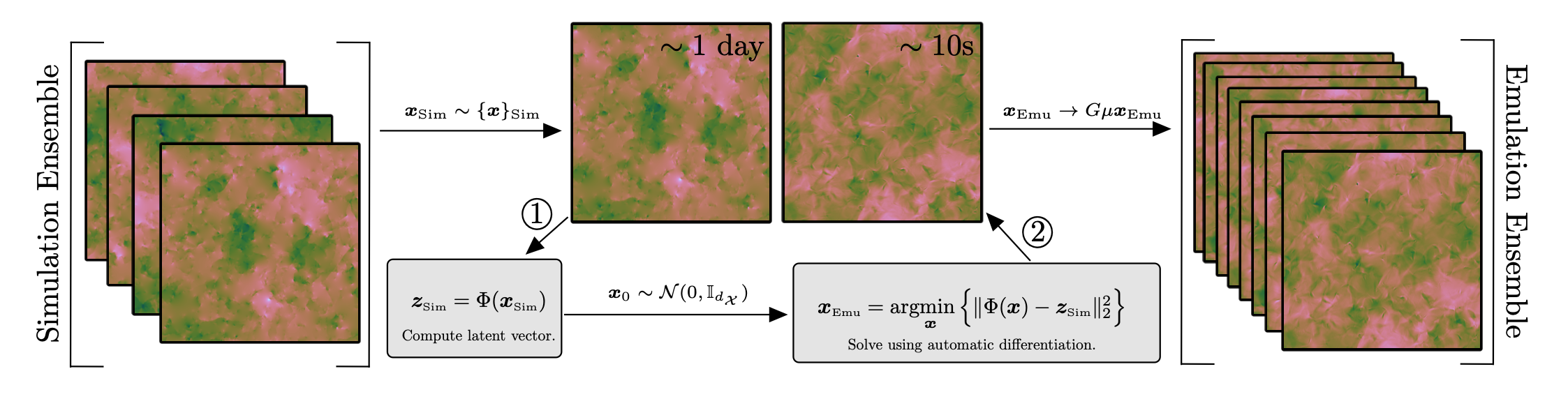
An overview of the process by which a small ensemble of simulated observables can be extremely augmented with emulated observables. In this case we consider cosmic string induced CMB anisotropies. In step 1 (compression) we simply draw uniformly from our simulated ensemble from which a target statistical representation (latent vector) z is calculated. In step 2 (synthesis) we exploit automatic differentation to iteratively recover emulated realisations.

Small-field Emulations

Below we compare a gallery of simulated Nambu-Goto planar cosmic string maps (left) against emulated maps (right). In all cases we generate emulations by the method outlined in the left panel of this poster. Each map on the left takes ~1 day to generate, whereas one on the right takes ~10s.

Gallery of simulated planar Nambu-Goto cosmic string induced CMB anisotropies. Each of these fields takes around 24 hours to generate, at a resolution of 1024x1024.

Gallery of emulated planar Nambu-Goto cosmic string induced CMB anisotropies. In each case we begin from the maximum entropy state (a random noise field) and minimse the least squares distance between the scattering statistics of our emulation and a single simulated field. In this sense we *match* the scattering statistics which are designed to capture complex non-Gaussian structure within such images. Each emulated field takes roughly 10s to produce, facilitating the inclusion of string induced anistropies in forthcoming large scale Bayesian analyses of the CMB.

Wide-Field Emulations

Full-sky emulation of Nambu-Goto strings through 3^rd generation scattering covariances (L=1024)

This animation demonstrates the full-sky emulation of Nambu-Goto cosmic string induced CMB anisotropies. We begin in the maximum entropy state (random noise) before matching the scattering covariances generated from a single Nambu-Goto simulation by least squares, which we optimize with adam. Typically, of order 20 iterations is sufficient to recover the relevant fine scale structure, with a wall-time of roughly 1 GPU hour compared to full simulations which can take up to 1 million CPU hours. This time saving unlocks, for example, the possible inclusion of faithfully generated string anisotropies in forthcoming Bayesian analyses of the CMB.

Example of a faithfully simulated full-sky signtaure of Nambu-Goto cosmic string induced CMB anisotropies. For reference, this single field required approximately 800,000 CPU hours to simulate.

Full-sky emulation of the cosmic web through 3^rd generation scattering covariances (L=512)

This animation demonstrates the full-sky emulation of the weak gravitational lensing convergence field, which is related to the distribution of dark matter on the celestial sphere. Again, we begin in the maximum entropy state before matching the scattering covariances calculated from a single simulation. In each case all covariance and both power- and bi-spectra are concurrent, and so the simulated and emulated fields are statistically indistinguishable. This method provides a new method by which very many simulations may be generated at a fraction of the computational cost for use in e.g. Bayesian inference.

Example of a simulated full-sky weak gravitational lensing convergence map. Notice the complex filamentary structure, or *cosmic web*, which is typically difficult to capture statistically.

Next generation scattering

Third generation scattering covariances

For our wide-field emulation we adopt next generation wavelet based scattering covariances on the sphere. These statistics are based on the directional covariances between wavelet convolutions at different scales, with an additional non-linearity in the form of the absolute value. This non-linearity scatters information towards lower resolutions, and so acts to compresses information into a useful summary statistic.

To efficiently execute wavelet convolutions on the sphere and rotation group they must be done in a generalised Fourier space. To emulate from this statistical representation requires automatic differentation through such transforms, which is non-trivial. We use the recently release S2FFT JAX package which provides efficient and automatically differentiable access to these terms.

A new generation of scattering statistics

Given an input signal "I" and a bank of wavelet filtes "psi" we first compute the wavelet coefficients "W" and their magnitude "M" by

W^{(q, \gamma)} = I * \Psi^{(q, \gamma)} \qquad \text{and} \qquad M^{(q, \gamma)} = | I * \Psi^{(q, \gamma)}| = |W^{(q, \gamma)}|

respectively, where "q" denotes scale and "gamma" denotes directionality. The third generation scattering covariances are then given by the following.

S_1^{(q, \gamma)} = \langle M^{(q, \gamma)} \rangle_{\omega} = \frac{1}{2\sqrt{\pi}}(M^{(q, \gamma)})_{00}

P_{00}^{(q, \gamma)} = \left \langle W^{(q, \gamma)} (W^{(q, \gamma)})^* \right\rangle_{\omega}

C_{01}^{(q_1, q_2, \gamma_1, \gamma_2)} = \left\langle W^{(q_2, \gamma_2)} (M^{(q_1, \gamma_1)} * \Psi^{(q_2, \gamma_2)} )^*\right\rangle_{\omega}

C_{11}^{(q_1, q_2, q_3, \gamma_1, \gamma_2, \gamma_3)} = \left\langle (M^{(q_1, \gamma_1)} * \Psi^{(q_3, \gamma_3)}) (M^{(q_2, \gamma_2)} * \Psi^{(q_3, \gamma_3)} )^*\right\rangle_{\omega}

The derivation of these statistics can be found in an upcoming paper Mousset et al 2023.

Each term in this designed representation correspond to progressively more non-Gaussian features on may reasonably expect from complex physical textures.

"S" controls the mean of the signal at each scale and in each direction, much in the same way that a scaling function controls the mean of a standard wavelet transform.
"P" controls for the power spectrum of the signal.
"C" controls the covariance between 2 (3) wavelet scales and directions, and therefore can capture highly filamentary non-Gaussian structure of the signal.

Latent emulation

By construction, our overall JAX transforms are automatically differentiable and therefore straightforward to emulate from, in the same way as for planar strings. At moderate resolution (L=1024) our Nambu-Goto full-sky emulations take ~20 minutes compared to the 800,000 CPU hours required by simulations.