Seager & Mallén-Ornelas (2003)
It is a common approach to derive stellar mass and radius by comparing observed quantities to expectations from stellar evolutionary models. Here, the observed quantities are the stellar density from the transit light curve (above) and the effective temperature obtained from spectroscopy.
Scroll down...
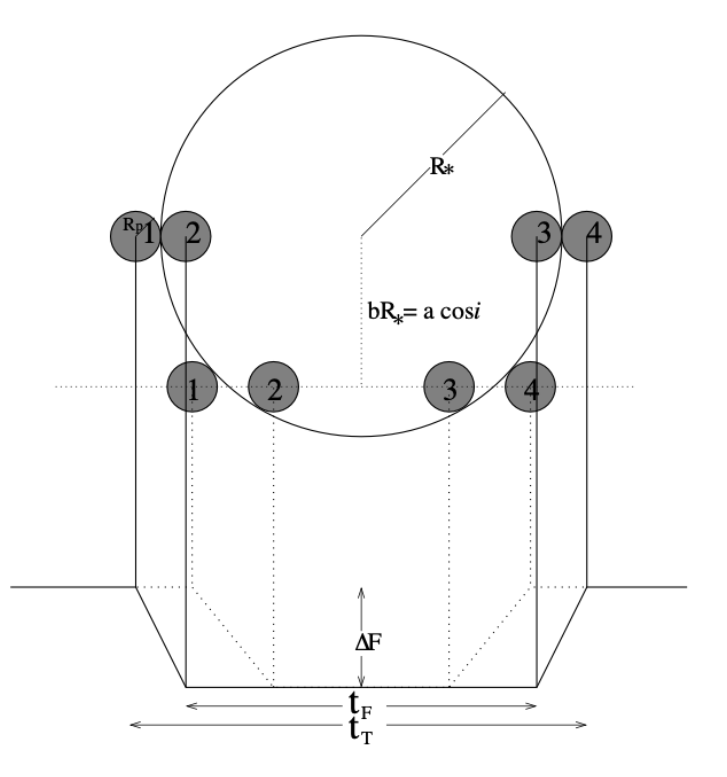
Stellar density can be directly determined from the transit geometry and timing encoded in the observed light curve (Seager & Mallén-Ornelas 2003, Sandford & Kipping 2017). It does not depend on details of stellar modelling.
Effective temperature is defined by the Stefan-Boltzmann law:
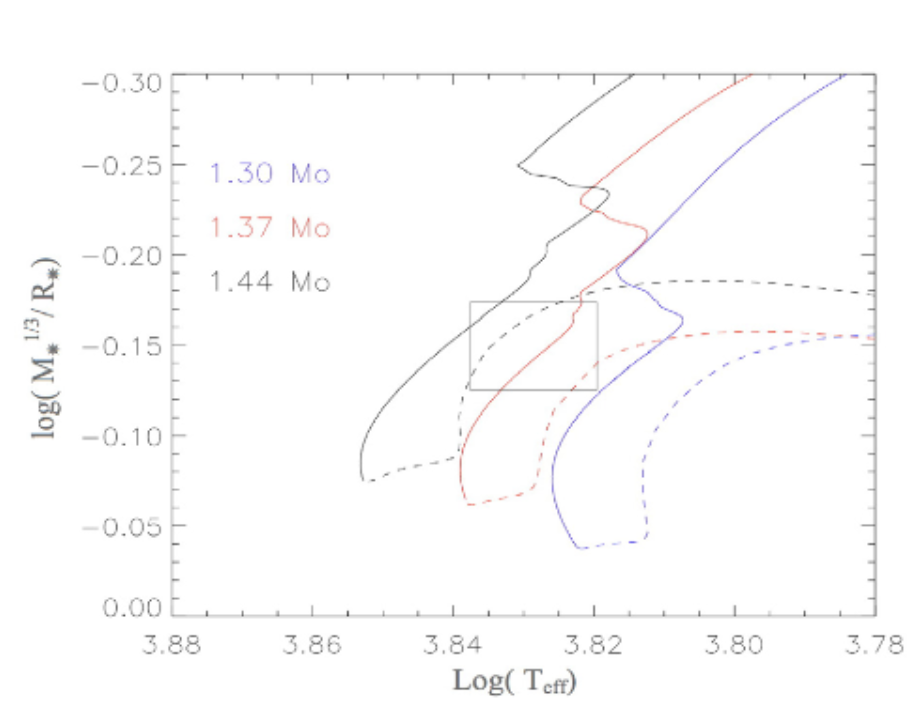
The stellar evolutionary models predict values for these quantities at different age and mass. These evolutionary tracks (solid lines in the figure below) are compared to the error bars of observations (open rectangle). Then, the radius can be computed from the density and the constrained mass.
Deleuil et al. (2008)
The caveat is that not only the evolutionary tracks are affected by uncertainties in stellar modeling but also the derived effective temperature depends on details of modelling stellar spectra lines. Thus, an independent prior on effective temperature is important.