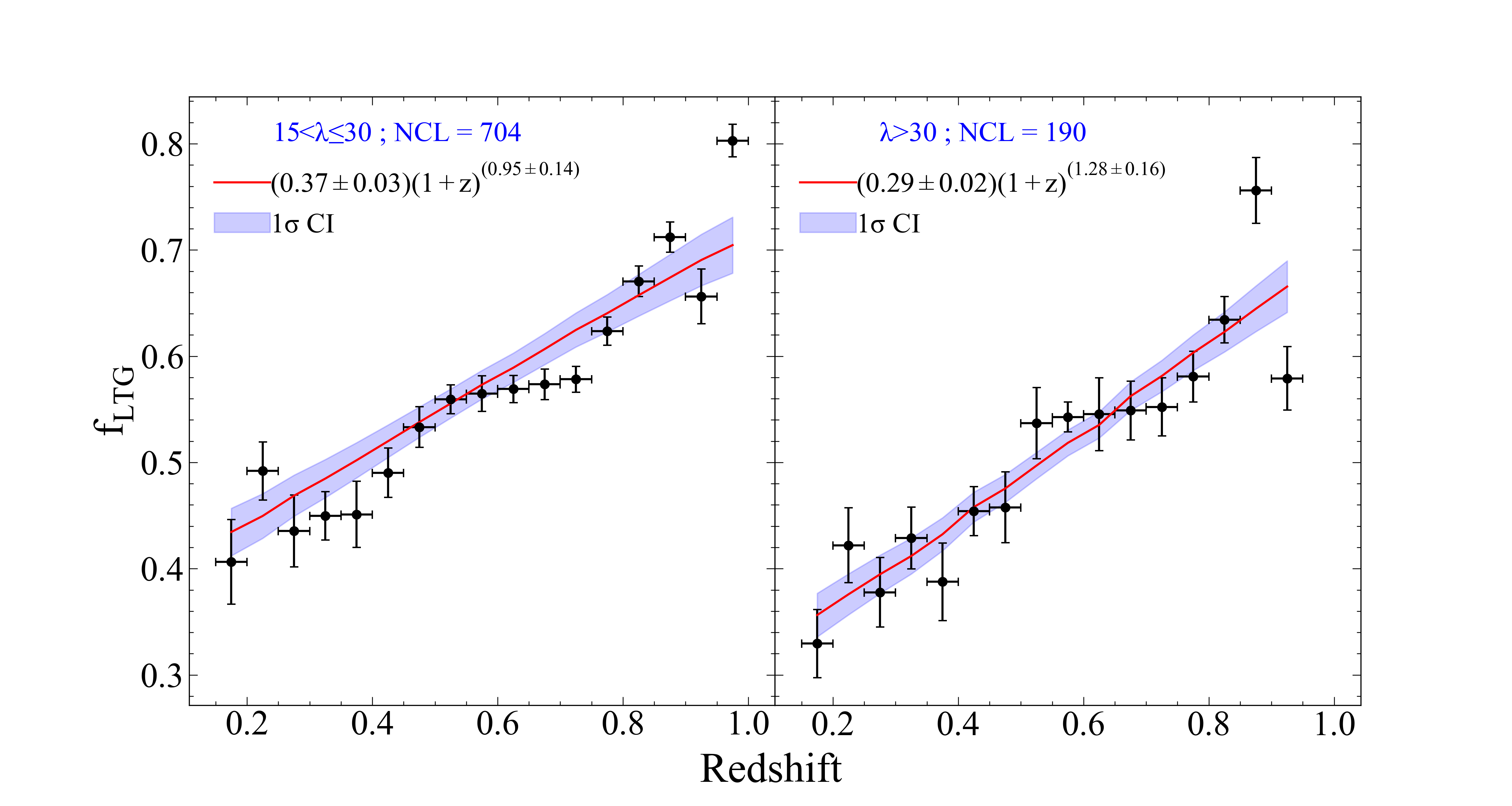
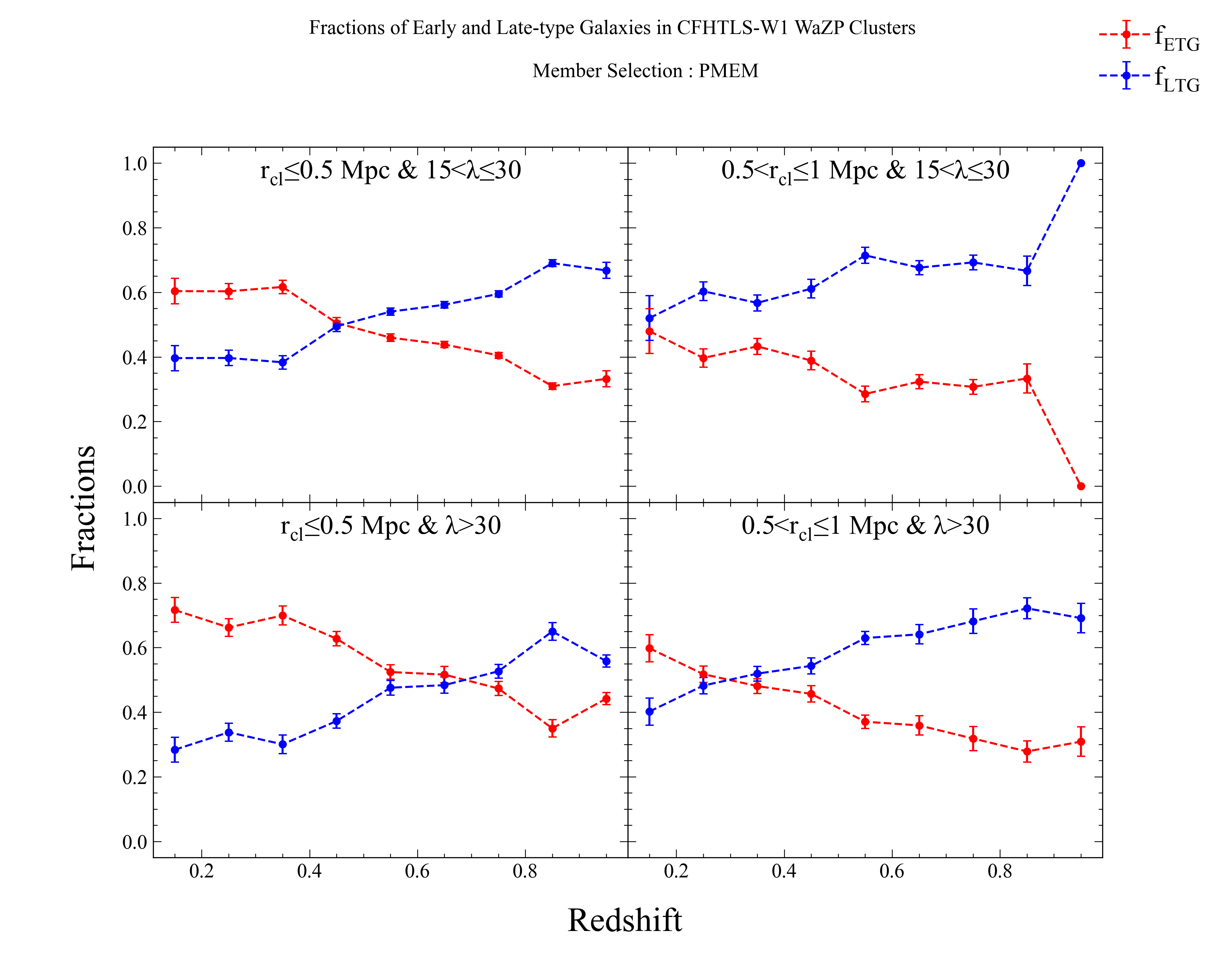
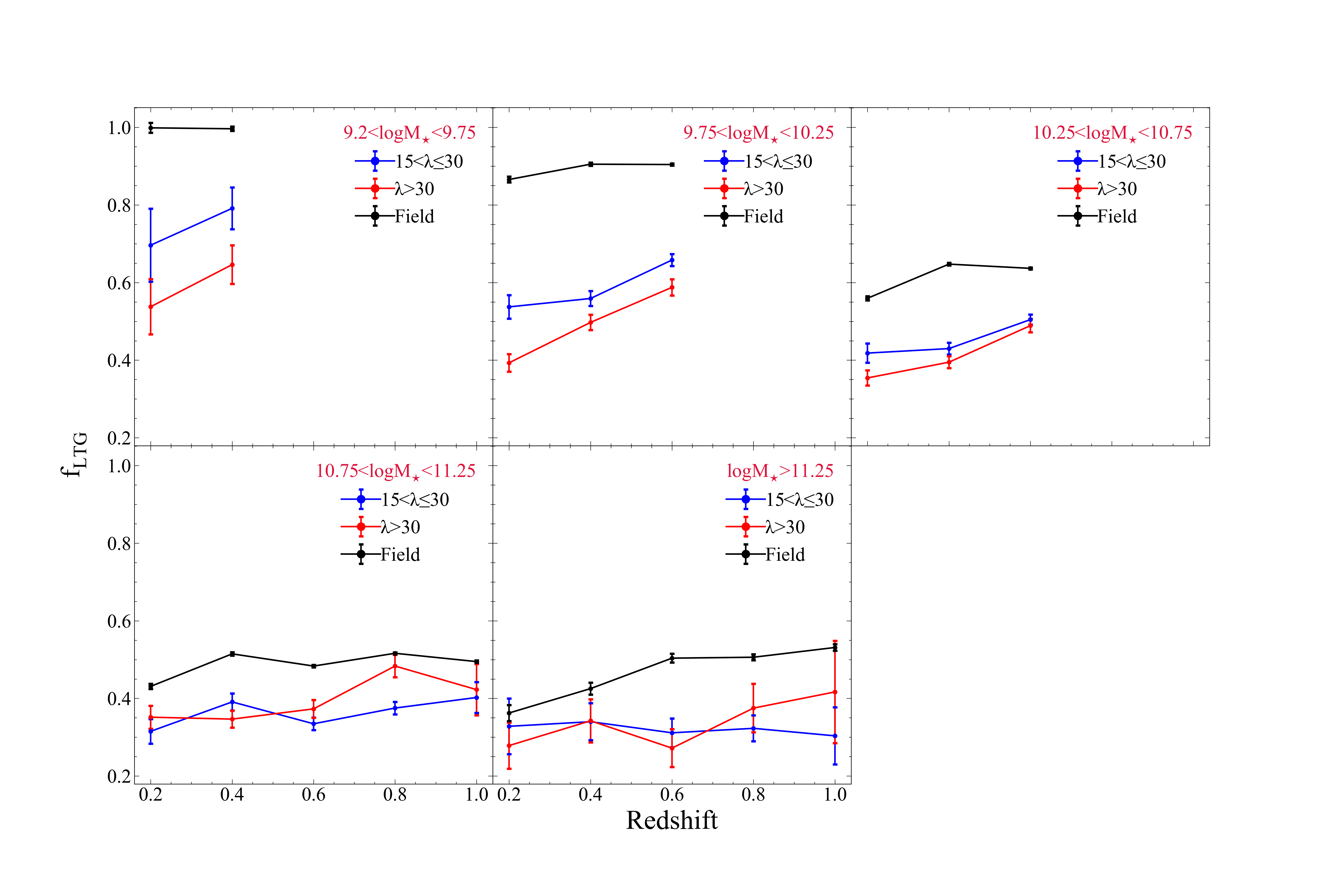
Once member galaxies are determined, we classify them analyzing their SED by implementing LePhare algorithm (Arnouts et al., 1999; Ilbert et al., 2006). There are 66 extrapolated SED templates derived from templates that of Coleman et al. (1980) and Kinney et al. (1996). As a by-product LePhare gives SED template solutions as a parameter called "MODE". Using this parameter, we separated members as early-types (Ell) to be MODE≤22, whereas late-types (Sp, Irr, SB) to be MODE>22. We then compute the fraction of both populations for each cluster as follows
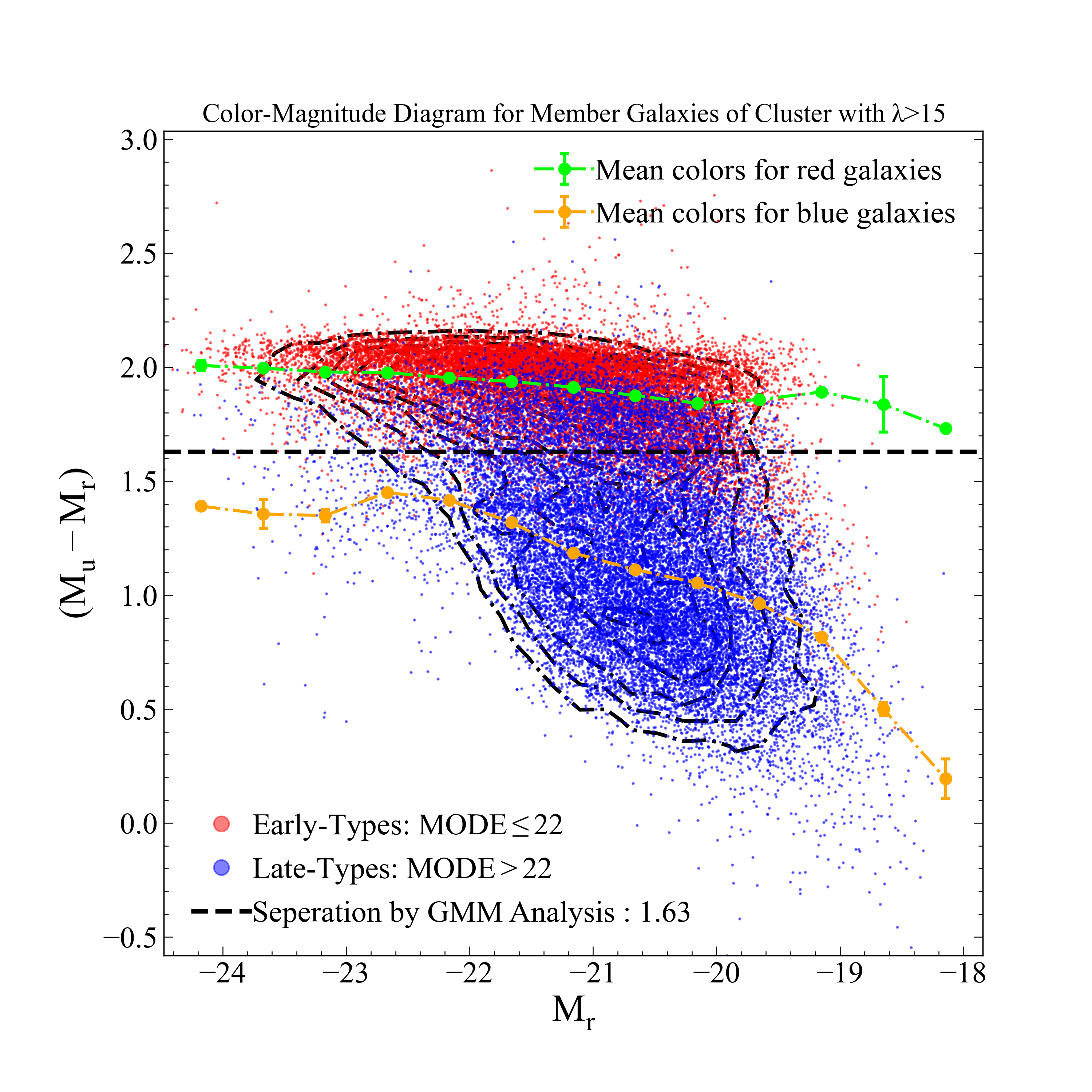
Figure 3 : Color-magnitude diagram for member galaxies. Red and blue dots indicate the galaxies defined as early-type and late-type, respectively. Dashed horizontal line is the color separation for red/blue galaxies obtained by GMM analysis. Green and orange dots show the mean (Mu-Mr) color for binned magnitudes for early-type and late-type galaxies, respectively.
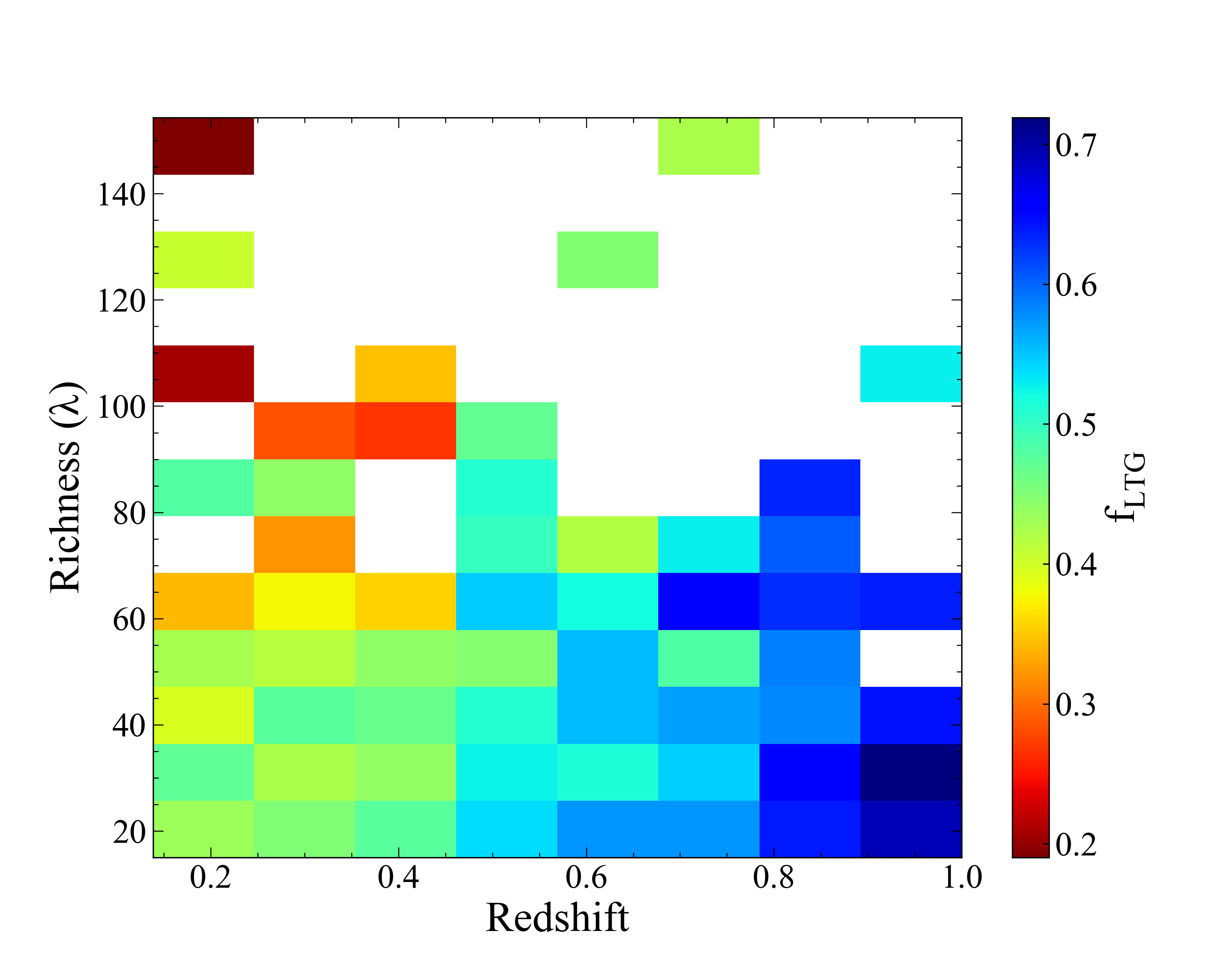
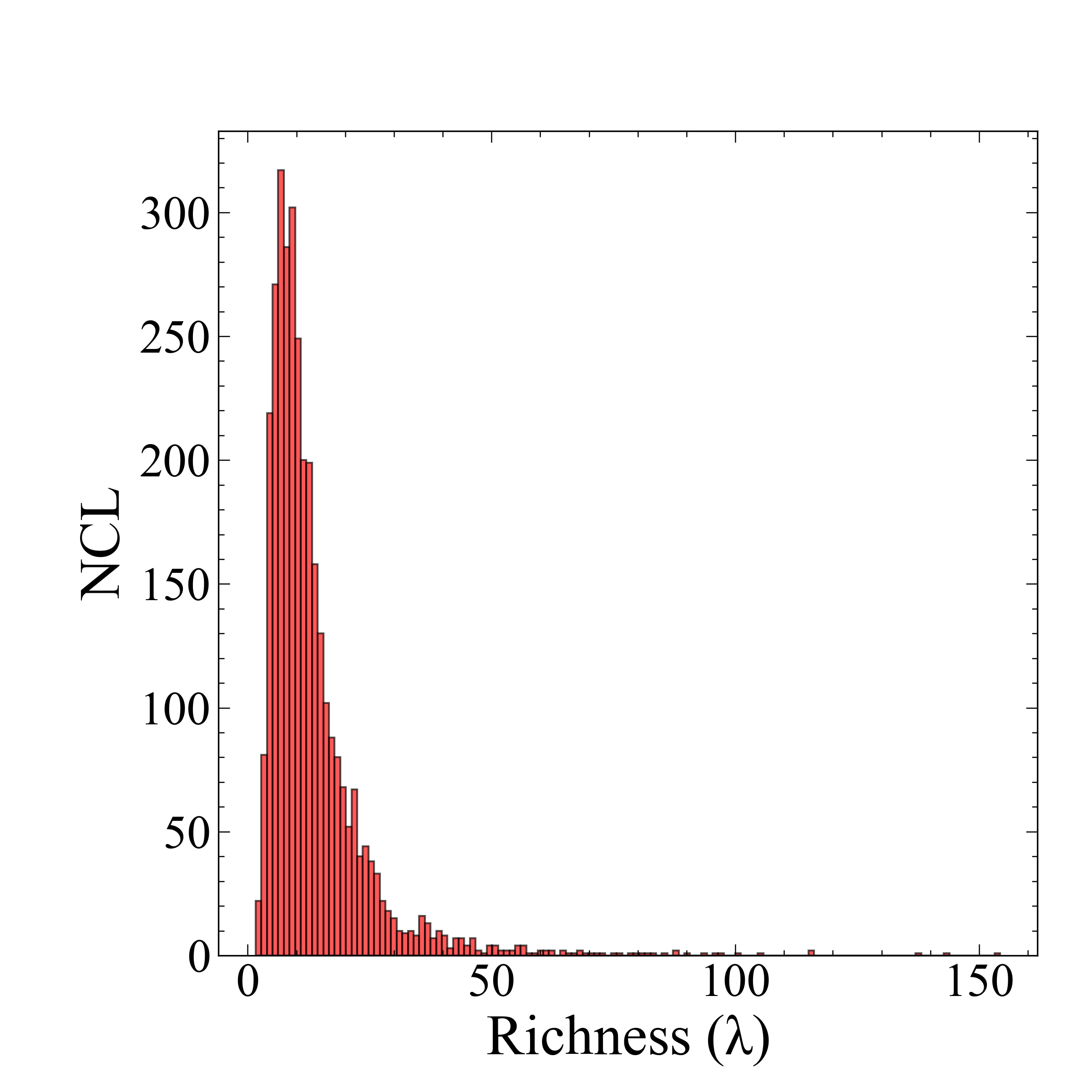
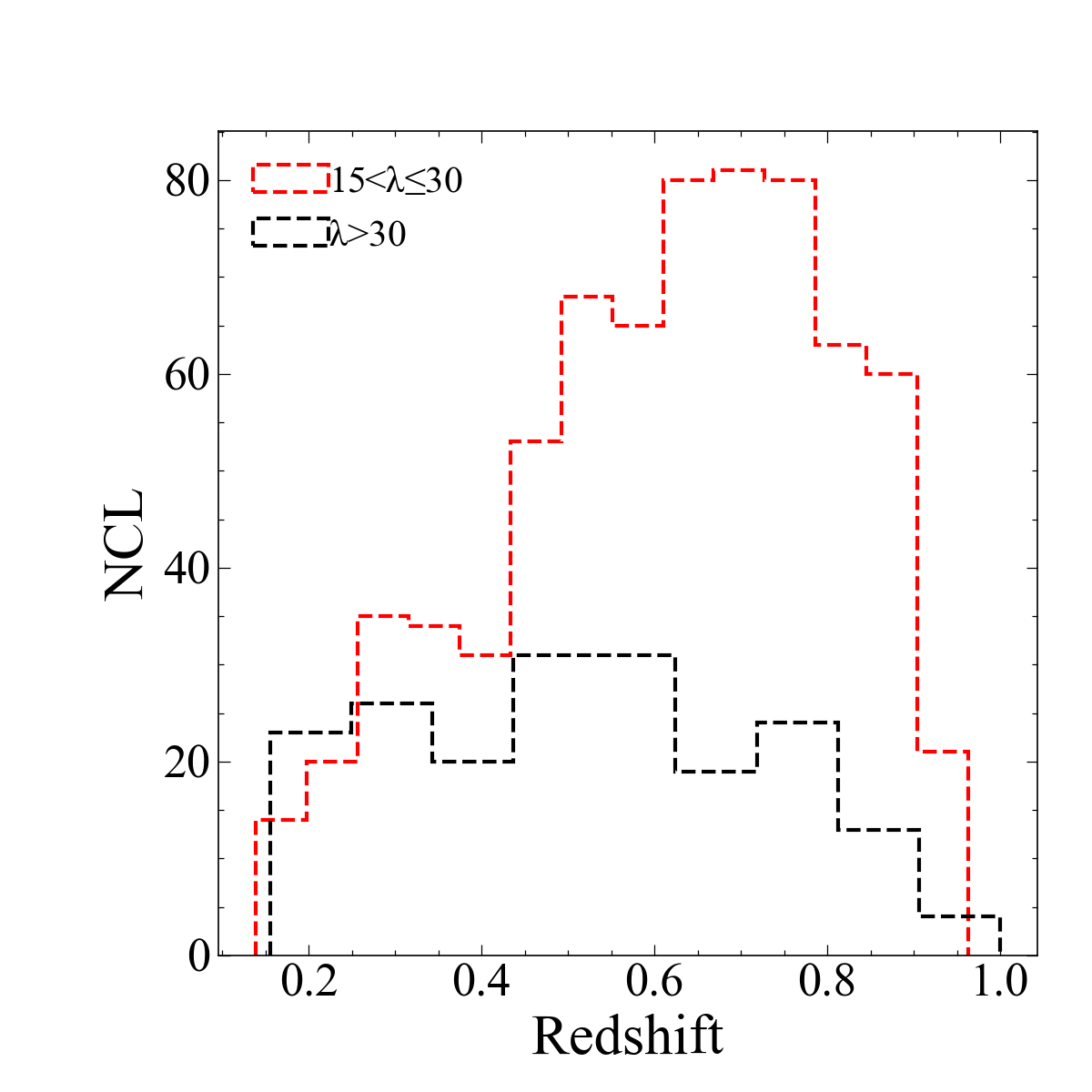
Figure 4 : Richness and redshift distribution of the clusters with λ>15 as a 2D histogram. The color codes represent the fraction late-type galaxies, the bluer the color, the higher fraction of late-type galaxies.