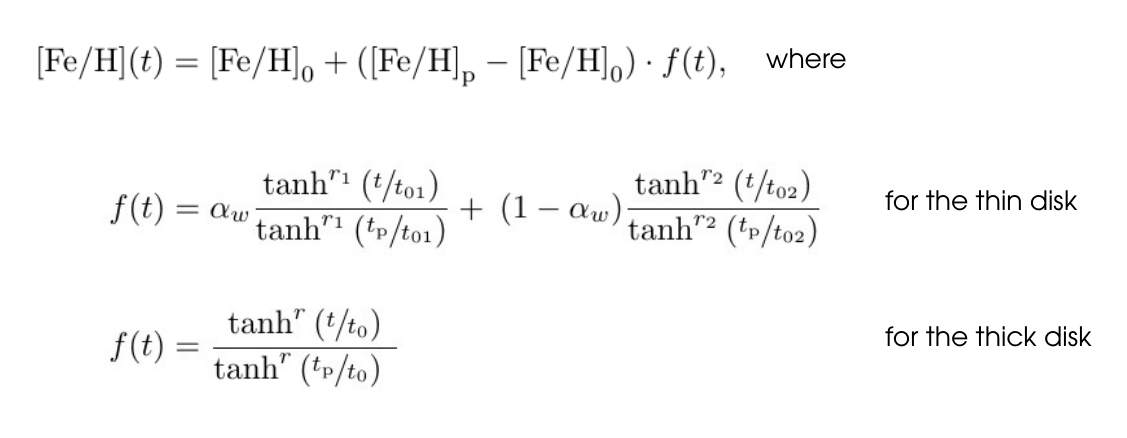Introduction
We develop a semi-analytic model of the Milky Way (MW) disk with a fine time resolution of 25 Myr (Just and Jahreiß 2010, Paper I). The Just-Jahreiß (JJ) model is based on an iterative solving of the Poisson equation and reconstructs a self-consistent pair of the total vertical gravitational potential and density. The thin disk is modeled in a presence of gas, thick disk, stellar halo, and dark matter (DM). The disk evolution is governed by four input functions: star formation rate (SFR), initial mass function (IMF), age-velocity dispersion relation (AVR), and age-metallicity relation (AMR).
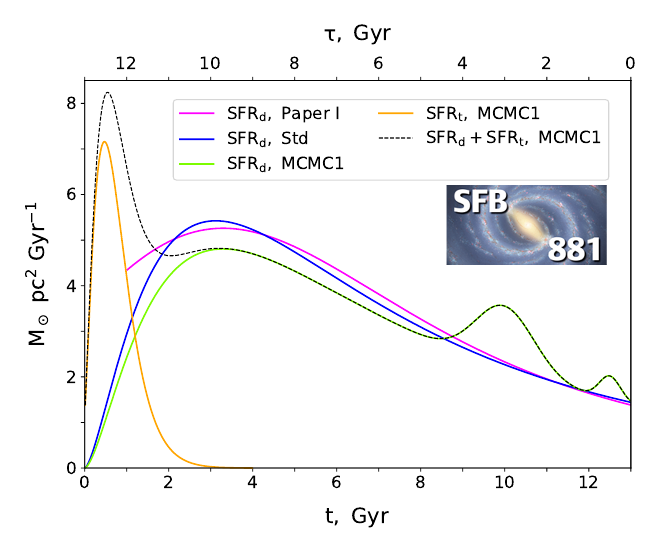
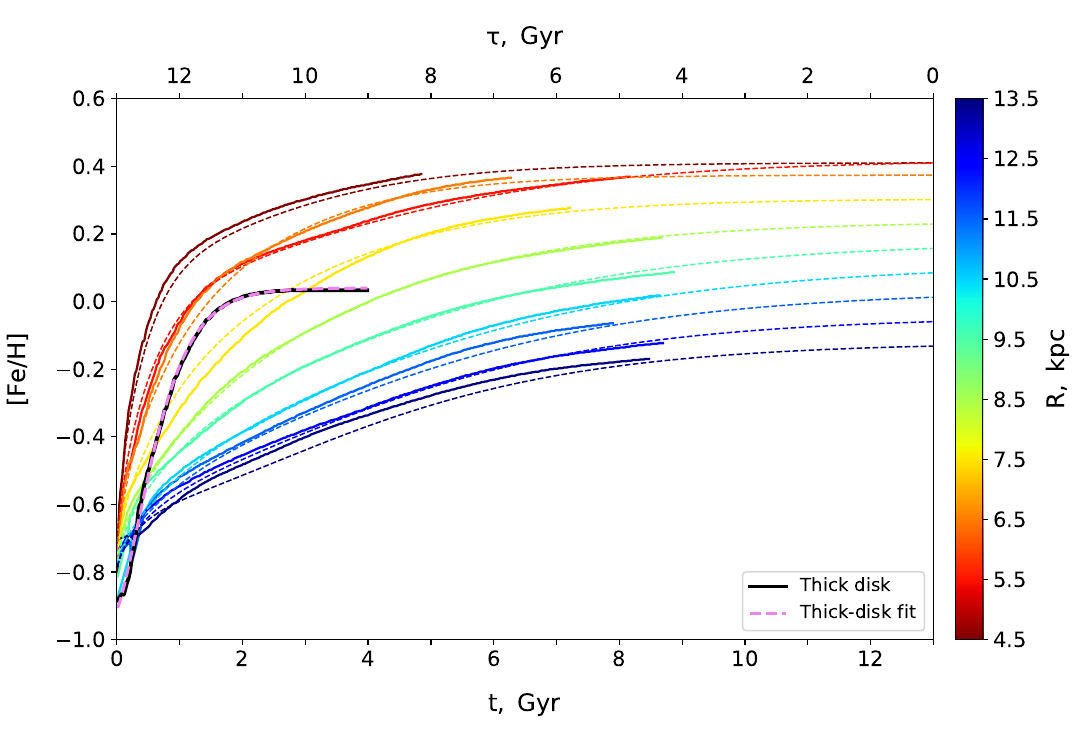
Figure 1. The normalized local thin-disk SFR as inferred from Gaia DR2 in Paper IV (green curve). The assumed thick-disk SFR is shown in orange, and the dashed black curve is the total disk SFR. The thin-disk SFR of the standard model (no extra SF bursts, best parameters from Papers I-III) is shown in blue. For comparison, we also plot the original thin-disk SFR from Paper I (magenta curve).
Local calibration based on Gaia (and other data)
The JJ model has been many times tested and calibrated against different data in the Solar neighborhood:
- In Just et al. (2011) (Paper II), we used star counts towards the north Galactic pole from the SDSS DR7 to optimize the SFR and thick-disk parameters.
- In Rybizki and Just (2015) (Paper III), we improved the IMF with the help of Hipparcos data complemented by an updated version of the CNS4 (Catalog of Nearby Stars).
- In Sysoliatina et al. (2018), we demonstrated a good model-to-data consistency (with a ~7.3-% discrepancy in terms of star counts) in the local 1-kpc height cylinder using stars from the RAVE DR5 and Gaia DR1 stars (TGAS).
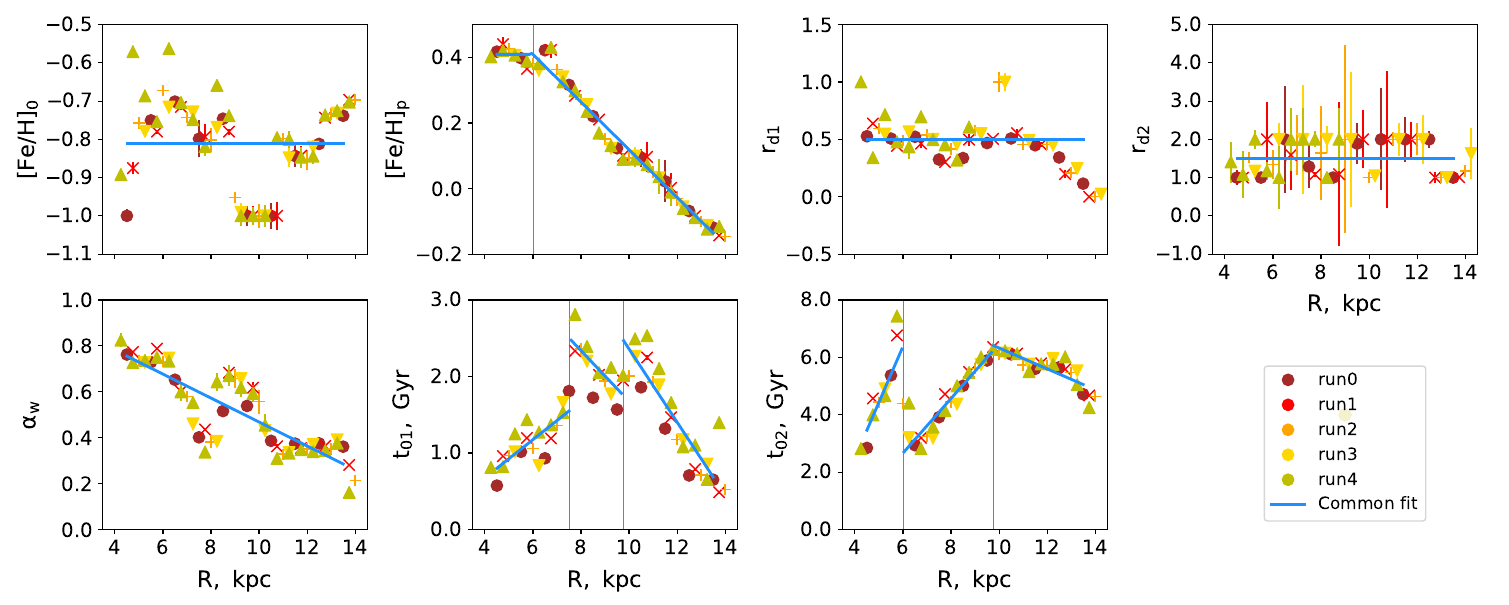
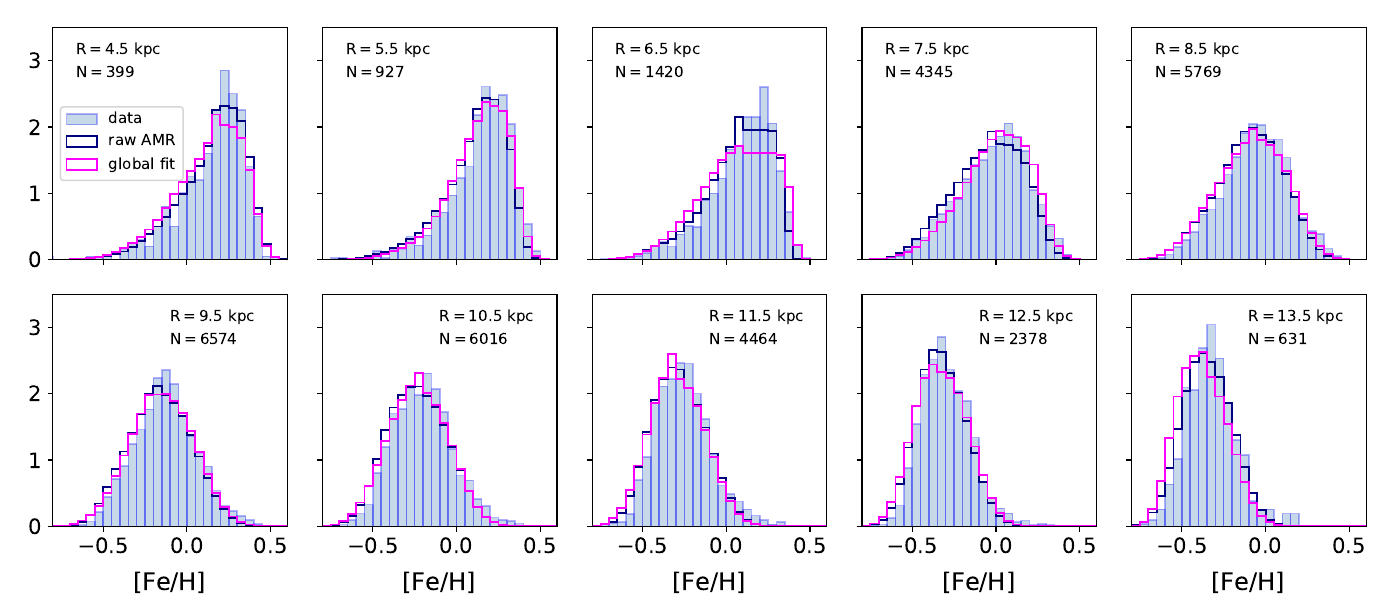
- Most recently, we used Gaia DR2 stars within 600 pc from the Sun and simultaneously optimized 22 model parameters within the Bayesian framework (Sysoliatina and Just 2021, Paper IV). We also calibrated the AMR against the local Red Clump (RC) sample from the APOGEE survey.
In Paper IV, we have identified two recent star formation (SF) burst episodes in the thin-disk evolutionary history, which happened ~0.5 Gyr and ~3 Gyr ago and left behind dynamically heated fossil populations. This interesting result is consistent with Mor et al. (2019) who found a single SF burst centered at the age of 2-3 Gyr. Also, Ruiz-Lara et al. (2020) report three SF enhancements 5.7 Gyr, 1.9 Gyr, and 1 Gyr ago, which were presumably triggered by recurrent passages of the Sagittarius dwarf galaxy.
More details on the local calibration of the JJ model can be found in our EAS2021 K-poster, "Dynamically hot recent star bursts in the Galactic disc".