Continuous gravitational waves from scalar boson clouds around Kerr black holes: observational issues and search strategies.

Lorenzo Pierini 1,2 , Riccardo  Felicetti 1

  • 1 La Sapienza University Of Rome, Rome
  • 2 INFN Roma, Rome

Abstract

The possibility that ultra-light boson clouds form around spinning black holes through the superradiance mechanism and then emit gravitational radiation, is extremely interesting. In the last years, a lot of work has been done to develop search procedures for these sources. In this talk, I will introduce some issues related to this kind of searches and their possible solutions. In particular, I will focus on the interesting scenario in which the superradiance affects a significant fraction of galactic black holes, resulting in clusters of signals with similar frequencies.

Boson clouds around Kerr black holes as gravitational wave sources

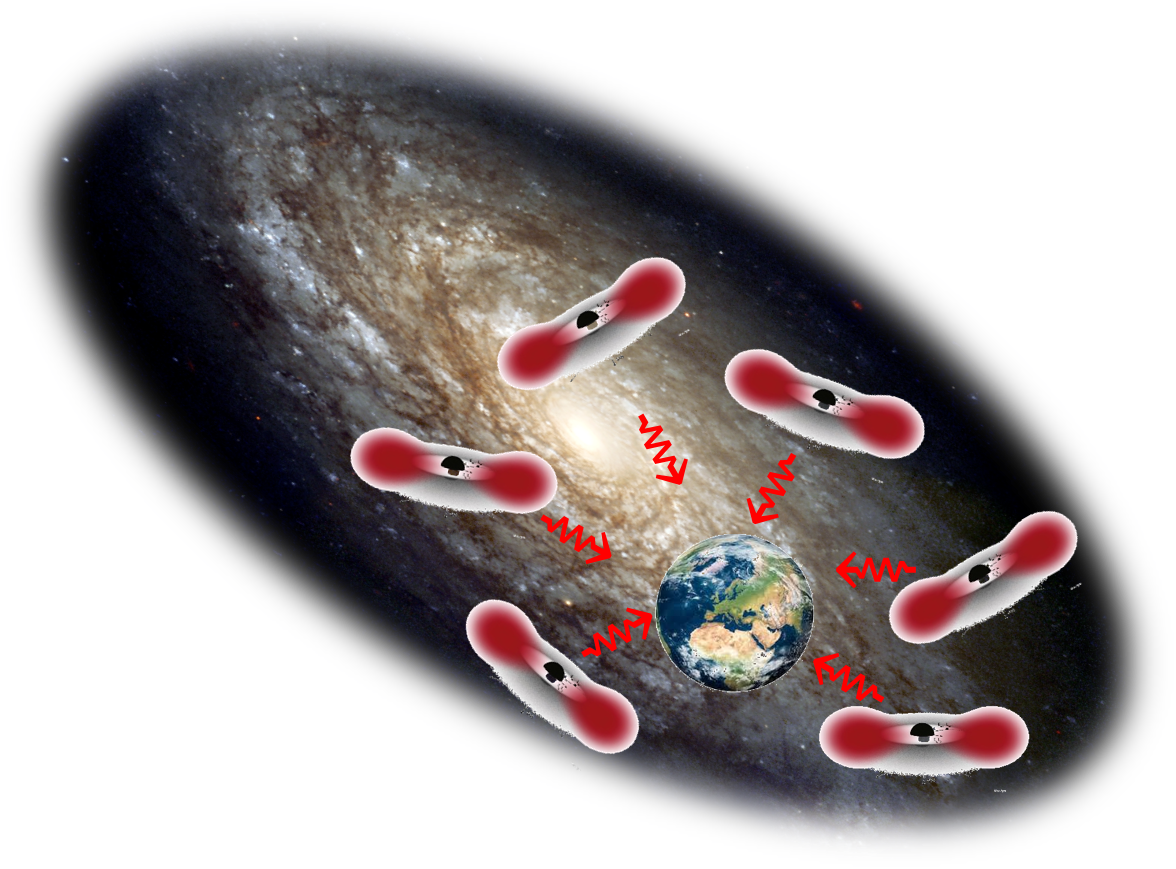
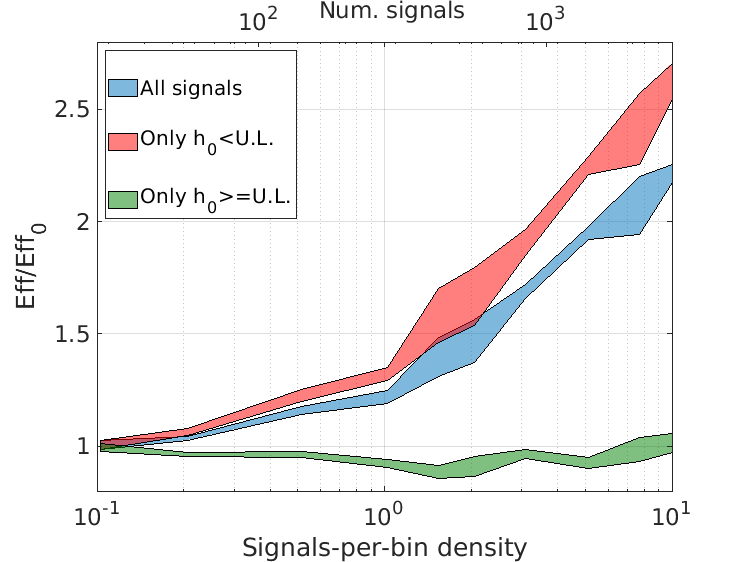
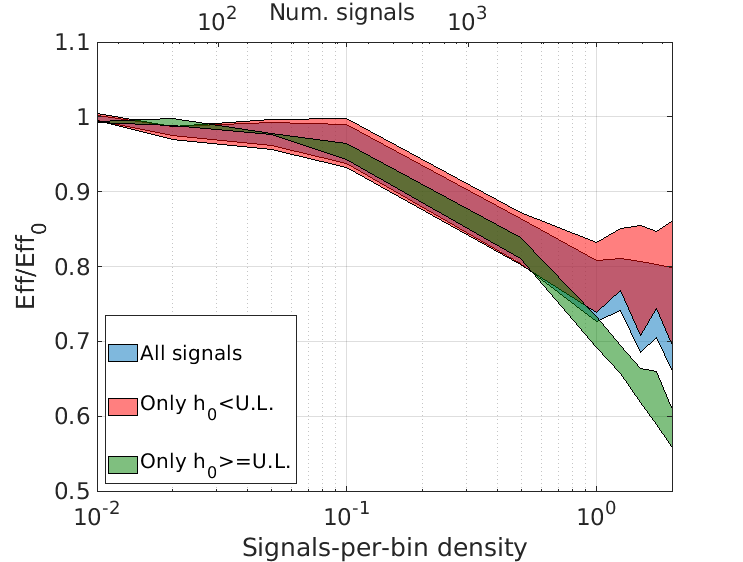
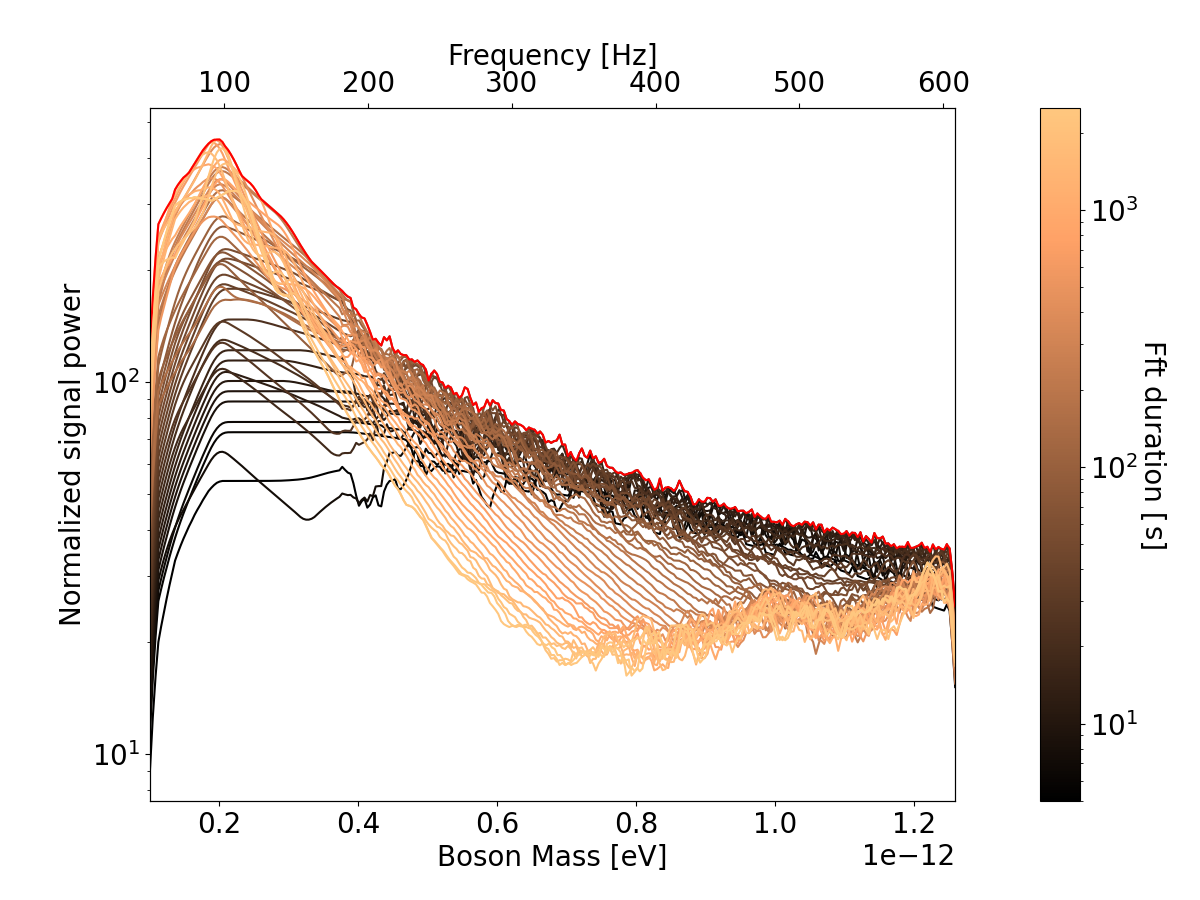
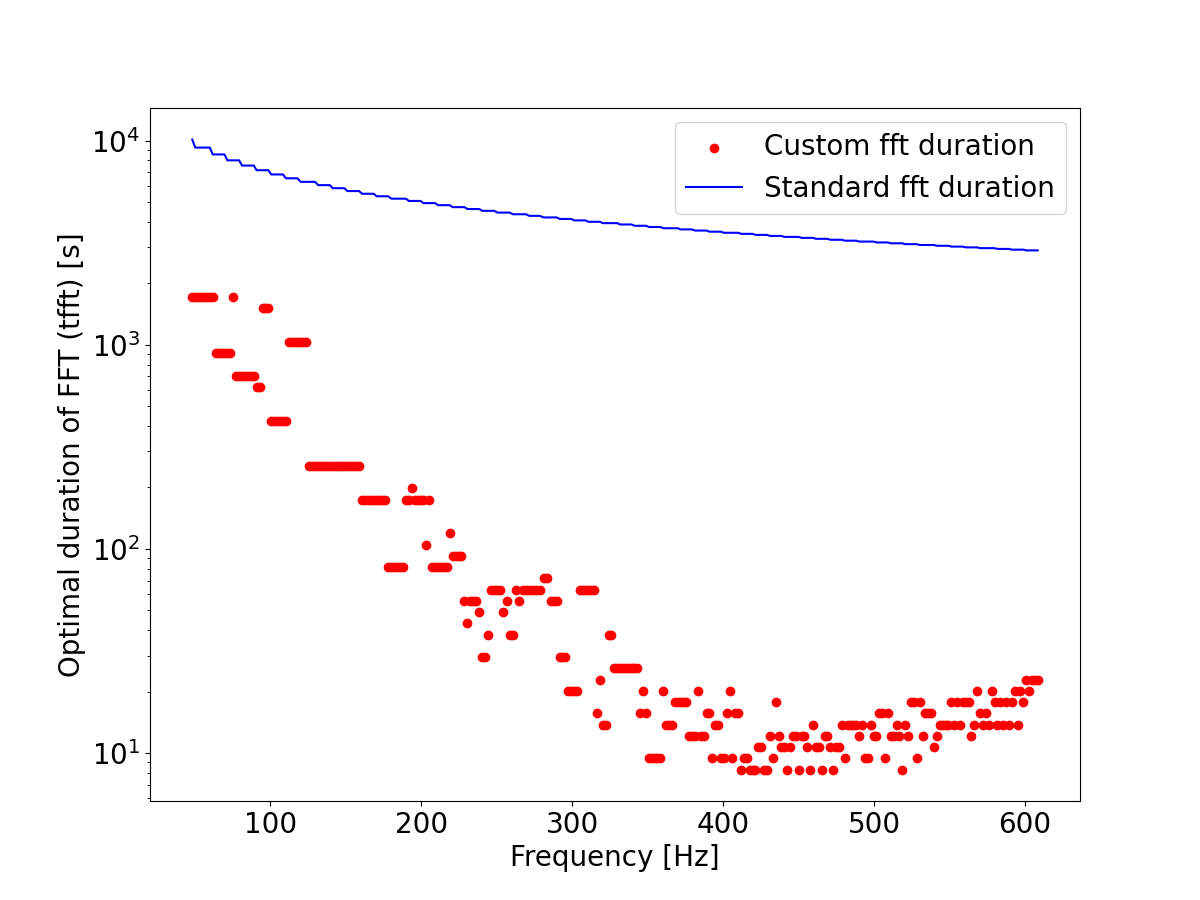
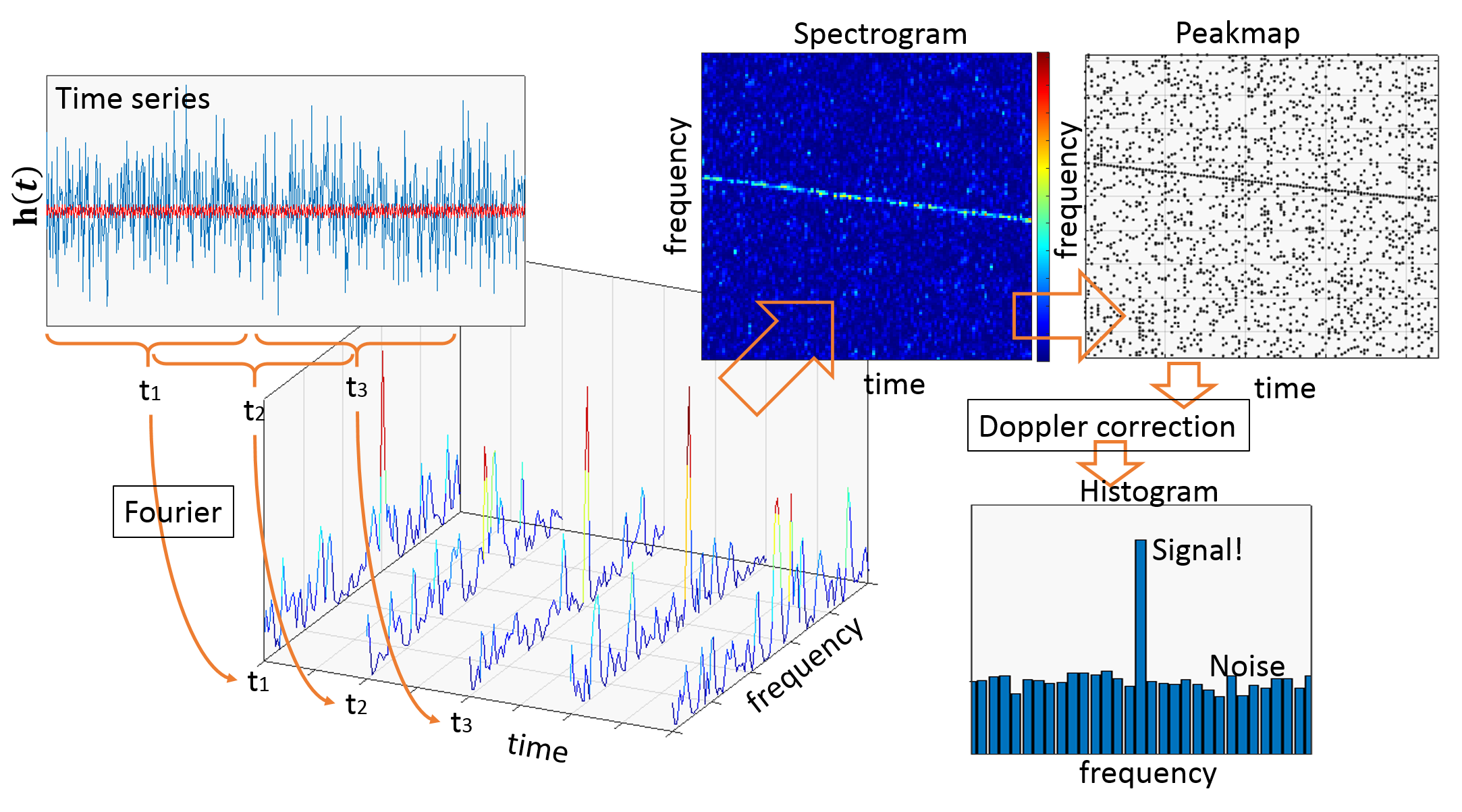
Ultralight bosons - like dark photons, QCD axion or axionlike particles - are some of the proposed dark matter candidates. If they exist, they would trigger superradiant instabilitiesround around spinning black holes if their Compton wavelenght is comparable  with the black hole size [1]. Under these
conditions, the bosonic field can bind to the BH, forming a “gravitational atom" cloud. After they are formed, these clouds dissipate and emit continuous gravitational waves through boson annihilation into gravitons.

Fine-structure constant of the gravitational atom:

\alpha=\frac{r_s}{\lambda}=\frac{G\,M_{BH}}{c^3}\frac{m_b}{\hbar}\qquad\qquad\qquad

Fundamental quantities:

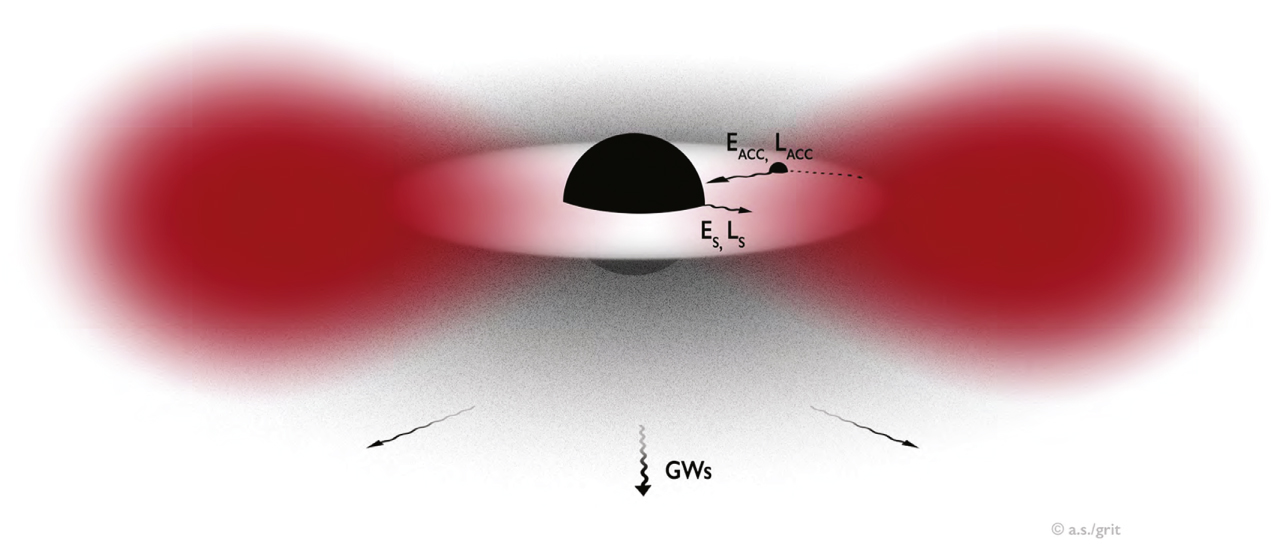
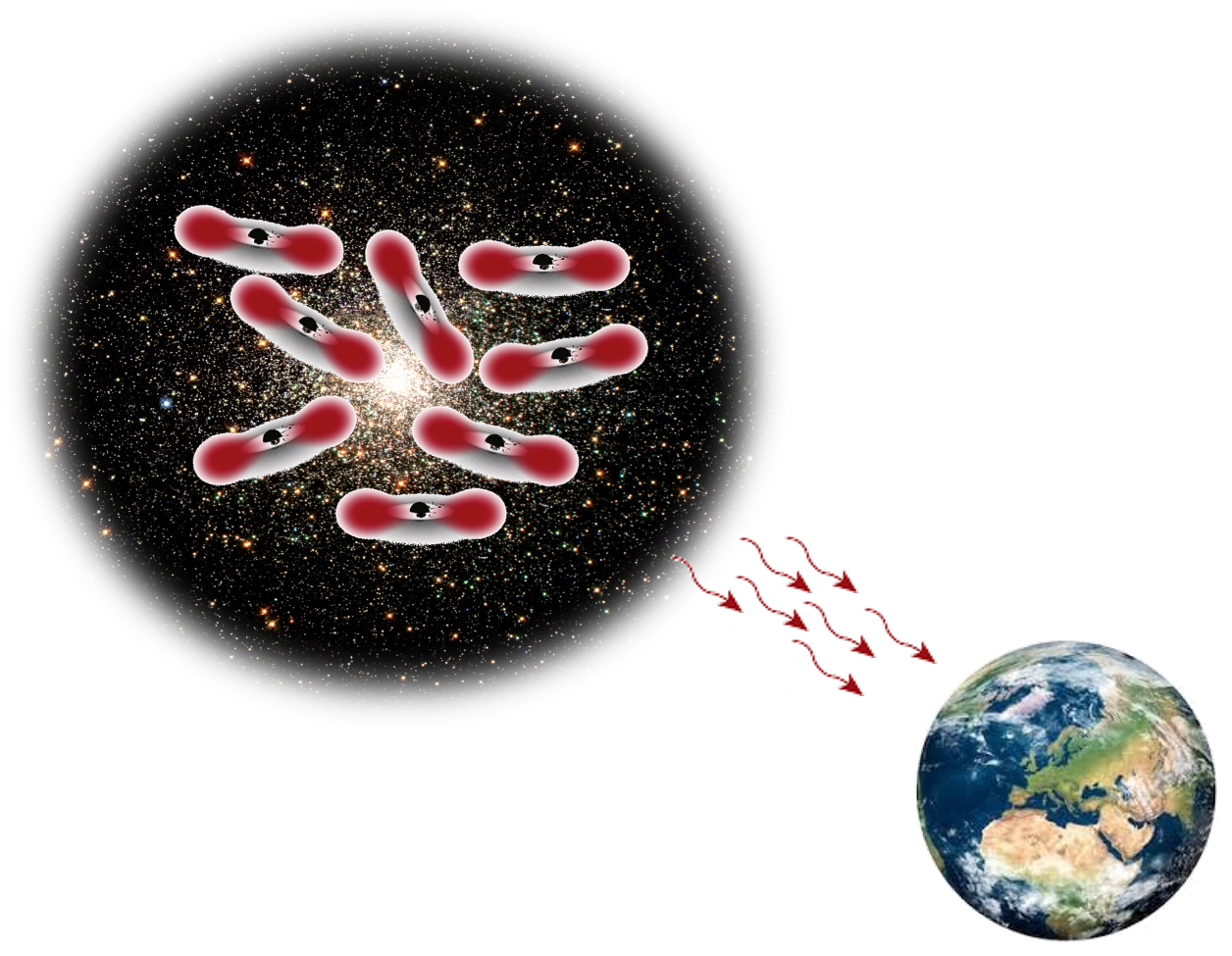
\begin{matrix} M_{BH}:\:\mathrm{black\:hole\:mass} & m_b:\:\mathrm{boson\:mass}\\ \chi_i:\:\mathrm{black\:hole\:dimentionless\:spin} & \chi_c\sim \frac{4\alpha}{1+4\alpha^2}\: :\:\mathrm{critical\:spin} \end{matrix}

Pictorial description of a bosonic cloud around a spinning BH.


Credits: Brito R. et al (2015) CQG 32(13), 134001.

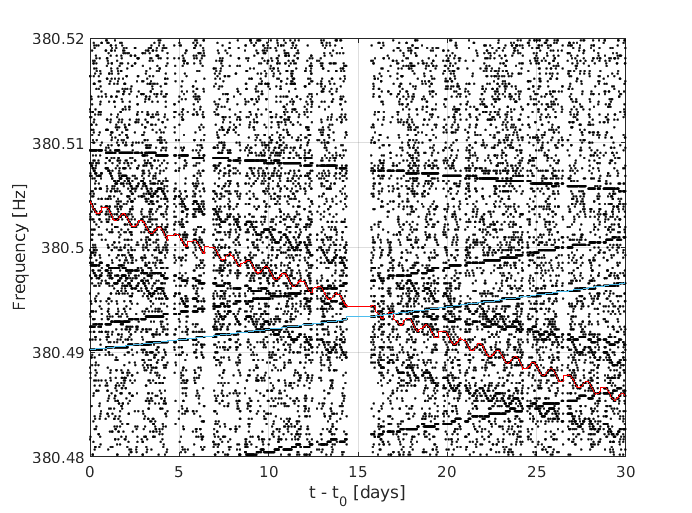
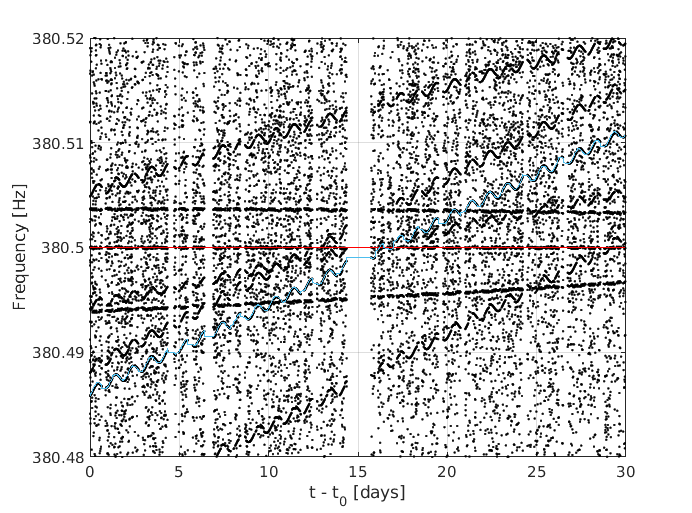
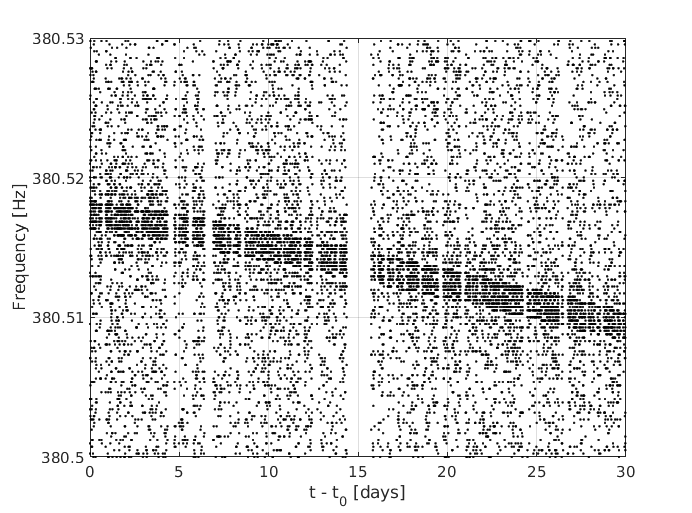
For scalar bosons, the expected wave has a lifetime ~104 years, with a frequency variation neglibible for the frequency resolution of all-sky searches. So, for our purpouses we can consider them as continuous, monochromatic waves.

h_0=3\cdot 10^{-24}\left(\frac{\alpha}{0.1}\right)^7\left(\frac{\chi_i-\chi_c}{0.5}\right)\left(\frac{M_{\mathrm{BH}}}{10M_\odot}\right)\left(\frac{1\mathrm{kpc}}{r}\right)
f_{\mathrm{gw}}=483 \mathrm{Hz} \left(\frac{m_b}{10^{-12}eV}\right)\left[1\:-\:7\cdot10^{-4}\left(\frac{M_{\mathrm{BH}}}{10M_\odot}\,\cdot\,\frac{m_b}{10^{-12}eV}\right)^2\right]

The case of galactic black holes

 

 

In the Milky Way ~108 black holes are expected to exist. If the superradiance mechanism affects a significative fraction of that black holes, we could have up to thousands of continuous wave emitters, from all possible sky directions.

In this situation, are we still able to resolve these signals, or would they act like a confusion noise?

Thanks to the different sky position, each signal gets a different Doppler modulation at the detector, due to the Earth motion with respect to the Solar System center of gravity. If we correct for Doppler effect for a given sky direction, only signals with the same location come back as monochromatic: all the others remain distorted.

So, within the limitations given by the sky and frequency resolution of the search, we are able to resolve the sources.

Left plot: Time-frequency peakmap of LIGO Livingston O3 data with 10 CW simulated signals, all with source frequency f0=380.5 Hz but different sky positions. Red and blue lines are superposed to 2 chosen signals to follow them.

Right plot: the same peakmap, with frequencies traslated to correct for Dopper effect for the signal marked with red line. Only the red signal turns back as monochromatic, whereas the others, including the blue one, get further distortion.

We performed a Monte Carlo, where we simulated the presence of a growing number of sources, from ~10 to ~3000, with proper frequencies in the range [100-400] Hz, into LIGO Livingston O2 data [3]. The signal frequencies are artificially spread in frequency intervals respectively ~0.06 Hz (bottom left figure) and ~0.8 Hz (bottom right figure) wide. We then evaluate the detection efficiency for each signal (see side figure). In the figures below, we plot the ratio of the detection efficiencies between clustered and  isolated signals. Coloured areas span from minimum to maximum values obtained at different frequencies.

From the plots, we can see that when signals concentrate in small frequency ranges (~0.06 Hz wide), the strongest signals do degrade, while the weakest reinforce each other, thus increasing the overall efficiency.

On the other side, when signals concentrate in larger frequency ranges (~0.8 Hz wide) we note an overall degradation of the efficiency, which corresponds to a sensitivity loss of at most ~13%.

Left plot: result oh the Monte Carlo simulation where from ~10 to ~3000 signals have been added in a frequency range ~0.06 Hz wide, covering signals-per-bin densities from 0.1 to 10. The green and red areas correspond to signals with amplitude respectively above and below the upper limits (ULs) found in [4], whereas the blue corresponds to whole set of signals.

Right plot: result oh the Monte Carlo simulation where from ~10 to ~3000 signals have been added in a frequency range ~0.8 Hz wide, covering signals-per-bin densities from 0.01 to 2. The green and red areas correspond to signals with amplitude respectively above and below the upper limits (ULs) found in [4], whereas the blue corresponds to whole set of signals.

These results are described in a paper submitted to PRD ("Impact of signal clusters in wide-band searches for continuous gravitational waves")

The case of black holes in globular clusters

It has been recently understood that globular clusters could host a population of ~102 solar-mass black holes. If they are affected by superradiance, we would have an high number of continuous waves emitters at very near frequencies and with the same sky localization.

In this case, we cannot distinguish them through their Doppler modulation.

So, we cannot resolve theese signals individually. Instead, we can do an ensemble detection.

Basic idea: build the peakmap starting from shorter data chunks, in order to have a lower frequency resolution. In this way, a growing number of signals fall into a same frequency bin. We search for a tradeoff between signal and noise contribution that maximizes the detecrion probability.

An optimal coherence time, depending on the boson mass (and consequently on the signal frequency), can be computed. In correspondance with this optimal duration, we achieve the maximum normalized power due to signals inside the frequency bins.

Left plot: multiple curves of the normalized signal power for different values of the FFT duration. The red curve follows the power maxima as a function of the boson mass.

Right plot: best FFT durations as a function of the signal frequency (scatter plot). The continuous line corresponds to the typical FFT length used in standard continuous wave searches.

References

[1]: Brito, R. et al. (2017). Gravitational wave searches for ultralight bosons with LIGO and LISA. Physical Review D, 96(6), 064050.

[2]: Abbott, R. et al. (2022). All-sky search for gravitational wave emission from scalar boson clouds around spinning black holes in LIGO O3 data. Physical Review D, 105(10), 102001.

[3]: Abbott, R. et al. (2021). Open data from the first and second observing runs of Advanced LIGO and Advanced Virgo. SoftwareX, 13, 100658.

[4]: Palomba, C. et al. (2019). Direct constraints on the ultralight boson mass from searches of continuous gravitational waves. Physical review letters, 123(17), 171101.

Search strategy

The raw data series is divided in short chunks with length ~103 s. For each data chunk we apply a cleaning procedure and compute the power spectral density.  From those, we construct the peakmap selecting only local maxima with normalized power above a fixed threshold. Then, we correct for Doppler effect through a frequency shift of the peakmap, according to a discrete sky grid. Finally, we evaluate frequency histograms from Doppler-corrected peakmaps, searching for excess of counts with respect to the noise background. Reference at [2].

Conclusions

We have shown that standard approaches to all-sky searches for continuous gravitational waves are robust with respect to the presence of signal clusters.

In particular, we have demonstrated that, in the case of numerous sources dislocated in our galaxy, these procedures are still able to recover the signals without suffering significant sensitivity losses.

Moreover, in the case of sources located in specific sky locations (e.g. nearby globular clusters), the detection probability can be increased by a suitable choice of the search coherence time.